Para achar uma dízima periódica, basta dividir o numerador pelo denominador da fração.
Quando temos uma fração e, ao efetuarmos a divisão do numerador pelo denominador, obtemos uma dízima periódica, dizemos, então, que essa fração que originou a dízima é a fração geratriz da dízima periódica.
Uma Dízima Periódica poderá ser representada de três formas diferentes :
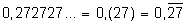
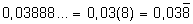
Os Casos da Conversão de Frações Ordinárias em Números Decimais
1º Caso: Número Decimal Exato
Uma fração ordinária e irredutível se transformará numa decimal exata quando seu denominador contiver apenas os fatores primos 2, 5 ou 2 e 5. O número de ordens, ou casas decimais, será dado pelo maior expoente dos fatores 2 ou 5.
Exemplo 1: A fração ordinária e irredutível 7/4 se converterá numa decimal exata já que o seu denominador 4 só contém o fator primo 2 ( 4 = 22 ). Essa decimal exata terá 2 casas decimais, já que o expoente do fator 2 é 2
Exemplo 2: A fração ordinária e irredutível 71/125 se converterá numa decimal exata já que o seu denominador 125 só contém o fator primo 5 ( 125 = 53 ). Essa decimal exata terá 3 casas decimais, já que o expoente do fator 5 é 3
Exemplo 3: A fração ordinária e irredutível 93/80 se converterá numa decimal exata já que o seu denominador 80 só contém os fatores primos 2 e 5 ( 40 = 24 x 5 ). Essa decimal exata terá 4 casas decimais, já que o expoente do fator 2 é 4
2º Caso: Dízima Periódica Simples
Uma fração ordinária e irredutível se transformará numa Dízima Periódica Simples quando seu denominador contiver apenas fatores primos diferentes dos fatores primos 2, 5 ou 2 e 5.
Exemplo 4: A fração ordinária e irredutível 16/9 se converterá numa Dízima Periódica Simples já que o seu denominador 9 só contém o fator primo 3 ( 9 = 32 )
Exemplo 5: A fração ordinária e irredutível 43/77 se converterá numa Dízima Periódica Simples já que o seu denominador 77 só contém os fatores primos 7 e 11 ( 77 = 7 x 11)
Exemplo 6: A fração ordinária e irredutível 8/117 se converterá numa Dízima Periódica Simples já que o seu denominador 117 só contém os fatores primos 3 e 13 ( 117 = 32 x 13)
3º Caso: Dízima Periódica Composta
Uma fração ordinária e irredutível se transformará numa Dízima Periódica Composta quando seu denominador, além dos fatores primos 2, 5 ou 2 e 5, contiver outros fatores primos quaisquer. O número de ordens, ou casas decimais, do ante-período será dado pelo maior expoente dos fatores 2 ou 5.
Exemplo 7: A fração ordinária e irredutível 2/15 se converterá numa Dízima Periódica Composta já que o seu denominador 15 contém além do fator primo 3, o fator primo 5 ( 15 = 3 x 5 ). Essa Dízima Periódica Composta terá um ante-período com 1 casa decimal, já que o expoente do fator 5 é 1.
Exemplo 8: A fração ordinária e irredutível 75/52 se converterá numa Dízima Periódica Composta já que o seu denominador 52 contém além do fator primo 2, o fator primo 13 ( 52 = 22 x 13 ). Essa Dízima Periódica Composta terá um ante-período com 2 casas decimais, já que o expoente do fator 2 é 2.
Exemplo 9: A fração ordinária e irredutível 7/680 se converterá numa Dízima Periódica Composta já que o seu denominador 340 contém além dos fatores primos 2 e 5, o fator primo 17 ( 680 = 23 x 5 x 17 ). Essa Dízima Periódica Composta terá um ante-período com 3 casas decimais, já que o expoente do fator 2 é 3
Geratriz de uma Dízima Periódica
Definimos Geratriz de uma dízima periódica como sendo a fração ordinária que originou essa dízima.
Exemplo 1: 1/3 é a geratriz da dízima periódica simples 0,333…
Exemplo 2: 23/30 é a geratriz da dízima periódica composta 0,7666…
Geratriz de uma Dízima Periódica Simples
A geratriz de uma dízima periódica simples é a fração cujo numerador é o período e cujo denominador é formado por tantos “noves” quantos forem os algarismos do período. Se a dízima possuir parte inteira, ela deve ser incluída à frente dessa fração, formando um número misto.
Exemplo 1 : Calcular a geratriz de 0,555…
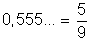
Exemplo 2: Calcular a geratriz de 1,363636…
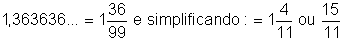
Exemplo 3: Calcular a geratriz de 2,006006006…
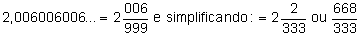
Geratriz de uma Dízima Periódica Composta
A geratriz de uma dízima periódica composta é a fração cujo numerador é o ante-período, acrescido do período e diminuído do ante-período e cujo denominador é formado por tantos “noves” quantos forem os algarismos do período, acrescido de tantos “zeros” quantos forem os algarismos do ante-período. Se a dízima possuir parte inteira, ela deve ser incluída à frente dessa fração, formando um número misto.
Exemplo 1: Calcular a geratriz de 0,03666…
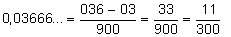
Exemplo 2: Calcular a geratriz de 1,4(30)
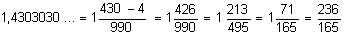
Exemplo 3: Calcular a geratriz de 2,14272727…
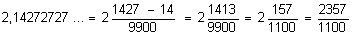
OBSERVAÇÃO IMPORTANTE: Em problemas e expressões, toda dízima periódica deve ser convertida em sua fração geratriz e somente aí serem efetuadas as operações necessárias.
Exercícios Propostos :
I – Determine a natureza de cada uma das frações quando convertidas em números decimais. Se a resposta for uma decimal exata, determine o número de casa decimais e se for uma dízima periódica composta determine o número de casa decimais do ante-período.
01) 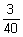 | 02) 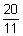 | 03)  |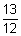
04) 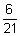 | 05) 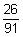 | 06)  |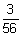
07) 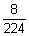 | 08) 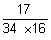 | 09)  |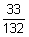
10) 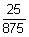 | 11) 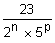 | 12)  |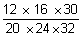
13 – Determine todos os valores possíveis de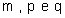 
para que a fração 
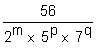se converta numa decimal exata com três casas decimais.
14 – Determine os valores naturais de m e p para a fração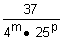 
se
converta numa decimal exata com 4 ordens decimais e tenha o maior valor possível.
15 – Que relação deve haver entre a e b de modo que a fração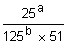 
seja a geratriz de uma dízima periódica simples.
16 – Determine o valor mínimo da soma dos naturais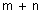 
de modo que a fração 
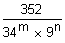se converta numa dízima periódica composta com 2 algarismos na parte não periódica.
II – Calcule as geratrizes das dízimas periódicas :
| 17) 0,555… | 18) 1,030303… |
| 19) 2,(36) | 20) 0,003003003… |
| 21) 1,(09) | 22) 2,027027027… |
| 23) 5,018018018… | 24) 0,0666… |
| 25) 1,04727272… | 26) 2,06818181… |
| 27) 1,32(4) | 28) 1,291666… |
| 29) 1,05(3) | 30) 3,61666… |
III – Calcule o valor das expressões abaixo :
31) 
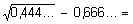32 – 0,(15) – ( 0,333…)2 =
Respostas dos Exercícios
| 01) D.E. – 3 casas | 02) D.P.S. | |
| 03) D.P.C. – 2 casas | 04) D.P.S. | |
| 05) D.P.S. | 06) D.P.C. – 3 casas | |
| 07) D.P.C. – 3 casas | 08) D.E. – 5 casas | |
| 09) D.E. – 2 casas | 10) D.P.C. – 2 casas | |
11) D.E. – n casas se n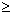 pD.E. – p casas se p | 12) D.E. – 3 casas | |
13)  | ||
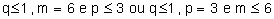14)  | ||
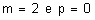15)  | ||
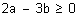16)  | ||
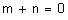17) 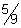 | 18)  | |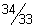
19) 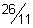 | 20)  | |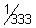
21) 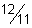 | 22)  | |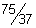
23) 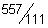 | 24)  | |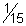
25) 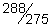 | 26)  | |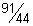
27) 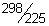 | 28)  | |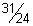
29) 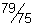 | 30)  | |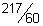
| 31) Zero | 32)  | |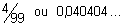
