01. Considere um conjunto de três pontos materiais definidos por m (x, y), onde m representa a massa em kg e x e y as coordenadas cartesianas, em metros. P1 = 2 (0,-1); P2 = 1 (1, 0); P3 = 2 (2, 6). O centro de massa do sistema dado, no gráfico, pelo ponto:
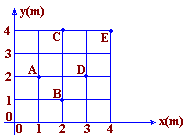
02. Determinar as coordenadas do Centro de Gravidade da placa homogênea, de espessura uniforme, indicada na figura abaixo.
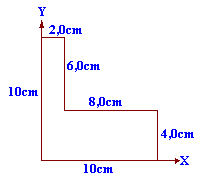
03. Duas partículas A e B estão inicialmente em repouso, separadas por 1,0m de distância. A massa de A é mA = 0,20kg e a de B é mB = 0,30kg. A e B se atraem mutuamente com forças constantes de intensidade F = 6,0 . 10-2N. Nenhuma força externa atua no sistema.
a) Descreva o que ocorre com o centro da massa do sistema.
b) A que distância da posição original de A as partículas colidem?
c) Calcule o módulo da velocidade relativa entre as partículas, no instante da colisão.
04. (FUND. CARLOS CHAGAS) Na figura abaixo estão representadas as velocidades vetoriais de duas pequenas esferas idênticas que constituem um sistema isolado. Qual a intensidade da velocidade do centro de massa do sistema?
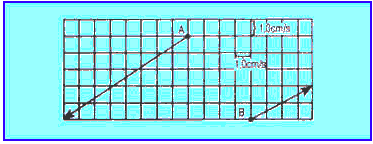
05. Considere duas esferas A e B constituindo um sistema físico. A esfera A está em repouso sobre um plano horizontal e a esfera B está em queda livre, num local onde a aceleração da gravidade vale 10 m/s2. A esfera A tem massa de 2,0kg e a esfera B tem massa de 3,0kg. Sabendo que a esfera B parte do repouso, calcule após 2,0s de queda livre:
a) o módulo de aceleração do centro de massa do sistema (A + B);
b) o módulo de velocidade do centro de massa do sistema (A + B).
06. (CESESP) Num circo, um equilibrista deseja levantar, apoiada em uma vareta, uma bandeja circular contendo um prato, um copo e uma garrafa cujas massas valem respectivamente 0,50kg, 0,10kg e 1,0kg. Escolhendo-se um sistema de eixos com origem no centro de gravidade da bandeja, as posições do prato, do copo e da garrafa são dadas respectivamente pelos pontos A, B e C da figura. Se a massa da bandeja for igual a 400g, em que posição (x, y) sob ela deve o equilibrista apoiar a vareta?
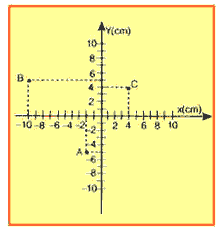
a) (-1, 0)
b) (1, 0)
c) (0, 1)
d) (2, 1)
e) (1, 1)
07. Considere a porta OABD indicada na figura. Metade da porta é de vidro e metade de madeira. A massa do vidro é 3/5 da massa da madeira.
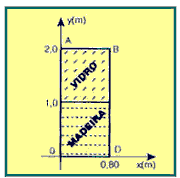
As coordenadas do centro de gravidade da porta são:
| xCM(m) | yCM(m) | |
| a) | 0,40 | 1,0 |
| b) | 0,80 | 2,0 |
| c) | 0 | 1,0 |
| d) | 0,40 | 7/8 |
| e) | 0,40 | 8/7 |
08. (CESGRANRIO) Seis peças de um jogo de dominó estão dispostas como na figura. Dos pontos indicados (F, G, H, I, J) o que melhor localiza o centro de massa desse conjunto é:
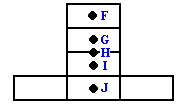
a) F
b) G
c) H
d) I
e) J
09. (ITA) As massas m1 = 3,0kg e m2 = 1,0kg foram fixadas nas extremidades de uma haste homogênea, de massa desprezível e 40cm de comprimento. Este sistema foi colocado verticalmente sobre uma superfície plana, perfeitamente lisa, conforme mostra a figura, e abandonado. A massa m1 colidirá com a superfície a uma distância x do ponto P dada por:
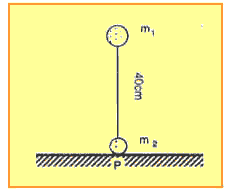
a) x = 0 (no ponto P)
b) x = 10cm
c) x = 20cm
d) x = 30cm
e) x = 40cm
10. Em um local onde o efeito do ar é desprezível e o campo de gravidade é uniforme, um martelo é lançado obliquamente para cima e o seu centro de massa (CM) descreve, em relação à superfície terrestre, a trajetória parabólica indicada.
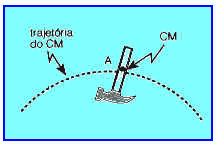
Se, na posição A, mostrada na figura, o batente do martelo se separasse do cabo, então:
a) o centro de massa do sistema (batente-cabo) passaria a desenvolver uma outra trajetória parabólica;
b) o centro de massa do sistema (batente-cabo) passaria a descrever uma trajetória retilínea;
c) o centro de massa do sistema (batente-cabo) continuaria descrevendo a mesma trajetória parabólica descrita pelo centro de massa do martelo, até que o batente e o cabo atinjam o solo;
d) o centro de massa do sistema (batente-cabo) continuaria descrevendo a mesma trajetória parabólica, descrita pelo centro de massa do martelo, até o instante em que um dos dois (batente ou cabo) atinja o solo;
e) nada se pode afirmar a respeito da trajetória do centro de massa do sistema (batente-cabo).
Leia o artigo: Centro de Massa
Respostas:
01 – Ponto A – yCM = 2m
02 – CM = (4, 1; 3,2) cm.
03 – a) CM em repouso
b) 0,60m
c) 1,0m/s
04 – 2,5 cm/s
05 – a) 6,0 m/s
b) 12 m/s2
| 06 – E | 07 – D | 08 – D | 09 – B | 10 – D |