Oscilações – Exercícios

01. Uma partícula executa movimento  harmônico simples de amplitude 10cm e frequência 2,0Hz. Pede-se calcular:

a) a pulsação do movimento;

b) a velocidade escalar da partícula ao passar em movimento progressivo pelo ponto de elongação 8,0cm;

c) a aceleração escalar da partícula nas condições do item anterior.

02. Podemos observar um movimento harmônico simples sempre que:

a) deixamos cair uma pedra do alto de um prédio;
b) lançamos uma caixa de fósforos sobre uma mesa horizontal e áspera;
c) alongamos lentamente uma mola elástica;
d) projetamos um movimento balístico no plano horizontal;
e) projetamos um movimento circular e uniforme sobre um diâmetro qualquer da circunferência.

03. (UNIMES) Um M.H.S. (movimento harmônico simples) é descrito pela função horária x = 5 cos (pt/2 + 3p/2), com x em metros e t em segundos. É correto afirmar que:

a) a amplitude do movimento é 10m;
b) a velocidade angular é 5p/2 rad/s;
c) a frequência do movimento é 0,25Hz;
d) o período do movimento é 0,50s;
e) a fase inicial é 3p radianos.

04. Um ponto oscila sobre um eixo Ox em movimento harmônico simples de amplitude a e frequência angular f. Das expressões seguintes a que relaciona corretamente a velocidade escalar V do ponto material em função de sua velocidade x é:

a) V² = f² (a² – x²)
b) V² = f² (a² + x²)
c) V² = f² (x² – a²)
d) V = f(a – x)
e) V = fx

05. Uma partícula descreve movimento harmônico simples de período 4,0s e amplitude 10cm. O módulo de sua velocidade ao passar por um ponto de trajetória, cuja elongação é 6,0 cm, vale:

a) 64p cm/s
b) 32p cm/s
c) 16p cm/s
d) 8,0p cm/s
e) 4,0p cm/s

06. (UFC) Considere um oscilador harmônico simples, unidimensional, do tipo massa-mola. Num primeiro momento ele é posto para oscilar com amplitude A, tendo frequência f₁ e energia mecânica E₁, e num segundo momento, com amplitude 2A, tendo frequência f₂ e energia mecânica E₂. Das opções abaixo indique aquela contém somente relações verdadeiras:

a) f₂ = f₁ e E₂ = 4E₁
b) f₂ = f₁ e E₂ = 2E₁
c) f₂ = 2f₁ e E₂ = 4E₁
d) f₂ = 2f₁ e E₂ = 2E₁
e) f₂ = 4f₁ e E₂ = 4E₁

07. Um pêndulo simples executa oscilações de pequena abertura angular de modo que a esfera pendular realiza um M.H.S.

Assinale a opção correta:

a) o período de oscilação independe do comprimento do pêndulo;
b) o período de oscilação é proporcional ao comprimento do pêndulo;
c) o período de oscilação independente do valor da aceleração da gravidade local;
d) o período de oscilação é inversamente proporcional ao valor da aceleração da gravidade local;
e) o período de oscilação independe da massa da esfera pendular.

08. (UFC) Considere dois osciladores, um pêndulo simples e um sistema massa-mola, que na superfície da Terra têm períodos iguais. Se levados para um planeta onde a gravidade na superfície é 1/4 da gravidade da superfície da Terra, podemos dizer que a razão entre o período do pêndulo e o período do sistema massa-mola, medidos na superfície do tal planeta, é:

a) 1/4
b) 1/2
c) 1
d) 2
e) 4

09. Para dobrar a frequência de oscilação de um pêndulo simples é suficiente:

a) transportá-lo para um planeta de aceleração da gravidade duas vezes maior;
b) transportá-lo para um planeta de aceleração da gravidade quatro vezes;
c) dobrar o comprimento do fio;
d) reduzir à quarta parte o comprimento do fio;
e) dobrar a massa pendular.

10. (UFU) Uma partícula oscila ligada a uma mola leve executando movimento harmônico simples de amplitude 2,0m. O diagrama seguinte representa a variação da energia potencial elástica (E_p) acumulada na mola em função da elongação da partícula (x).

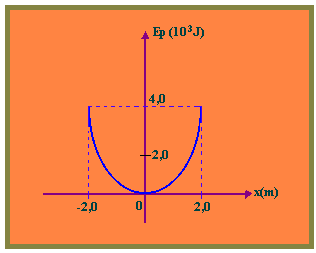
Pode-se afirmar que a energia cinética da partícula no ponto de elongação x = 1,0m, vale:

a) 3,0 . 10³J
b) 2,0 . 10³
c) 1,5 . 10³J
d) 1,0 . 10³J
e) 5,0 . 10²J

Leia o artigo: Oscilações

Respostas:

01 – a) 4p rad/s

1. b) 24p cm/s
2. c) -128 p²cm/s²