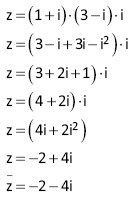Números Complexos – Exercícios

01. Se i é a unidade imaginária do conjunto dos números complexos, então o complexo (4 · i³ + 3 · i² + 2 · i + 1) é:

A) 6 + 4i
B) 1 + 2i
C) 2 + 2i
D) – 2 + 2i
E) – 2 – 2i

02. Considere o número complexo z= (1 + 3i) / (1 − i). A forma algébrica de z é dada por:

A) z = –1 + 2i
B) z = 1 – 2i
C) z = –2 + 1
D) z = –2 + 4i
E) z = –1 + 4i

03. Considere os números complexos z = 2 · (cos 30° + isen 30°) e u = z⁵. Os pontos P e Q são os afixos (ou imagens) dos complexos z e u, respectivamente. O ponto médio do segmento  tem coordenadas iguais a:

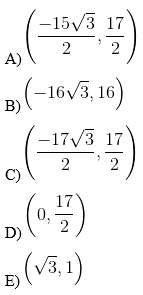
04. Considere os números complexos z = 3 · (cos6° + isen6°) e u = 5 · (cos50° + isen50°). A forma trigonométrica do complexo z · u é igual a:

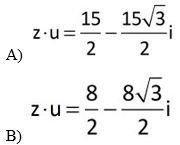
C) z · u = (cos (56°) + isen (56°))
D) z · u = 8 (cos (56°) + isen (56°))
E) z · u = 15 (cos (56°) + isen (56°))

05. O número complexo (1 + i)³⁶ é:

A) – 2¹⁸
B) 2¹⁸
C) 1 + i
D) 1 – i
E) 1

06. Considere o número complexo z = (a – 3) + (b – 5)i, em que a e b são números reais, e i é a unidade imaginária dos conjuntos dos números complexos. A condição para que z seja um número real não nulo é que:

A) b ≠ 5.
B) a = 3 e b ≠ 5.
C) a ≠ 3 e b ≠ 5.
D) a = 3 e b = 5.
E)  a ≠ 3 e b = 5.

07. O complexo (K + i) / (1 – Ki) , em que k é um número real e i é a unidade imaginária dos números complexos, é:

A) Ki
B) 1
C) – 1
D) i
E) – i

08. Considere o número complexo z = 1 + 8i. O produto z · , em que  é o conjugado de z, é:

A) – 63 + 16 i
B) – 63 – 16 i
C) – 63
D) 2
E) 65

09.  Considere o complexo z = 1 + i, em que i é a unidade imaginária. O complexo z¹⁴ é igual a:

A) 128i
B) – 128i
C) 0
D) 2
E) -128

10. Considere o complexo z = (1 + i) . (3 − i) . i, em que i é a unidade imaginária do conjunto dos números complexos. O conjugado de z é o complexo:

A) −2−4i
B) −2+4i
C) 2−4i
D) −2+2i
E) −2−2i

Respostas e resoluções dos exercícios

01: E

4 · i³ + 3 · i² + 2 · i + 1 = 4 (– i) – 3 + 2i + 1 = – 2 – 2i

02: A

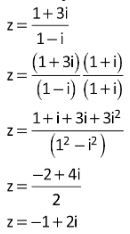
03: A

04: E

z = 3 · (cos6° + isen6°); u = 5 · (cos50° + isen50°)
z · u = 3 · (cos6° + isen6°) · 5 · (cos50° + isen50°)
z · u = 3 · 5 · (cos (6° + 50°) + isen (6° + 50°)
z · u = 15 · (cos (56°) + isen (56°))

05: A

06: E

z = (a – 3) + (b – 5)i
z será um número real não nulo se a parte imaginária for igual a zero e a parte real for diferente de zero.
Parte imaginária de z: b – 5
b – 5 = 0
b = 5.
Parte real diferente de zero: (a – 3) ≠ 0 ⇒ a ≠ 3
O complexo z é real não nulo se a ≠ 3 e b = 5.

07: D

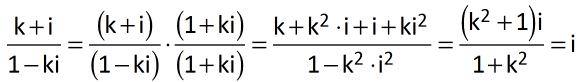
08: E

09: B

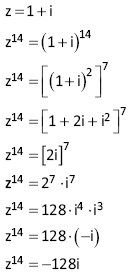
10: A