01. (FEI – MAUÁ) Secciona-se uma pirâmide regular de altura h por um plano paralelo à base, a uma distância x do vértice. Pede-se x de modo que a áreas laterais da pirâmide se altura x e do tronco de pirâmide de altura h – x sejam iguais.
02. (EUMT – LONDRINA) O volume de ar contido em um galpão com a forma e as dimensões dadas pela figura abaixo é:
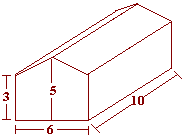 |
a) 300
b) 240
c) 225
d) 210
e) 180
03. (MAUÁ) Dado o Tetraedro de aresta L, determine, em função de L, o volume V do cone circular circunscrito, isto é, do cone que tem vértice do Tetraedro e base circunscrita à face do Tetraedro.
04. (MAUÁ) Dado um Tetraedro regular de aresta L, determine, em função de L, a área lateral A do cilindro reto circunscrito, isto é, do cilindro que tem uma base circunscrevendo uma face do Tetraedro e altura igual à altura do Tetraedro.
05. (LONDRINA) O tetraedro regular ABCD tem centro O. O ângulo diedro de faces OAB e OAC mede:
a) 30°
b) 60°
c) 120°
d) 135°
e) 150°
06. (SJRP – JUNDIAI) Os vértices de um tetraedro regular de volume 1m³ são centros das faces de outro tetraedro regular. O volume deste outro tetraedro vale:
a) 1 m³
b) 3m³
c) 9m³
d) 27m³
e) 81m³
07. (MAUÁ) Na pirâmide VABC os ângulos AVB, BVC e CVA são retos. Calcular a distância de V ao Plano ABC sabendo-se que VA = VB = VC = 1m.
08. (OSEC) Um prisma e uma pirâmide tem bases com a mesma área. Se o volume do prisma é o dobro do volume da pirâmide, a altura da pirâmide será:
a) O triplo da do prisma.
b) O dobro da do prisma.
c) O triplo da metade da do prisma.
d) O dobro da terça parte da do prisma.
e) n.d.a
09. (UnB) Sejam Pi e P2 duas pirâmides de mesma altura. A base de Pi é um quadrado e a de P2 um triângulo de área igual a do quadrado. Então, a área lateral de Pi é:
a) sempre maior do que a de P2;
b) sempre menor do que a de P2;
c) sempre igual a de P2;
d) n.d.a.
Leia o artigo: Geometria
Respostas:
01.
![]()
02. B
03.
![]()
04.
![]()
05. D
06. D
07.
![]()
08. C
09. D