01. Resolver o sistema abaixo pela Regra de Cramer.
![]()
02. Resolver o sistema abaixo pela Regra de Cramer.
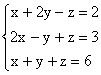
03. (UESP) Se o terno (x0, y0, z0) é a solução do sistema abaixo, então 3×0 + 5y0 + 4z0 é igual a:
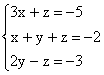
a) -8
b) -7
c) -6
d) -5
e) -4
04. Calcular a característica da matriz abaixo:
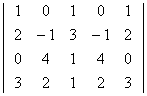
05. O sistema abaixo:
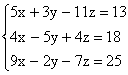
a) só apresenta a solução trivial;
b) é possível e determinado não tendo solução trivial;
c) é possível e indeterminado;
d) é impossível;
e) admite a solução (1; 2; 1)
06. O sistema abaixo:
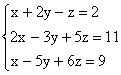
a) é impossível;
b) é possível e determinado;
c) é possível e indeterminado;
d) admite apenas a solução (1; 2; 3);
e) admite a solução (2; 0; 0)
07. (UEL) O sistema abaixo, de incógnitas x e y, é:
a) impossível, para todo k real diferente de -21;
b) possível e indeterminado, para todo k real diferente de -63;
c) possível e determinado, para todo k real diferente de -21;
d) possível e indeterminado, para todo k real diferente de -3;
e) possível e determinado, para todo k real diferente de -1 e -63.
08. Considere o seguinte sistema de equações de incógnitas x e y:
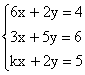
Esse sistema tem uma única solução para certo número real k que é um:
a) quadrado perfeito
b) número primo
c) número racional não inteiro
d) número negativo
e) múltiplo de 5
09. Se tivermos o sistema abaixo, então x + y + z + t é igual a:
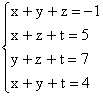
a) -1
b) 7
c) 5
d) 4
e) 5/9
10. Determinar m para que o sistema abaixo tenha apenas a solução trivial.
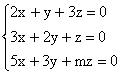
Leia o artigo: Sistemas Lineares
Respostas:
01 – (2; 3)
02 – (1; 2; 3)
| 03 – B | 04 – 3 | 05 – D | 06 – C |
| 07 – C | 08 – A | 09 – C | 10 – m ¹ 4 |