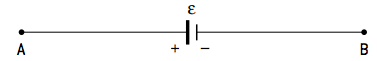Muitos circuitos elétricos não podem ser analisados simplesmente pela substituição de resistores por outros equivalentes. O problema foi há muito resolvido pelo físico alemão Gustav Robert Kirchhoff (1824-1887), que criou leis capazes de resolver circuitos mais complexos. São as duas leis de Kirchhoff. Essas leis podem ser aplicadas em qualquer circuito, mesmo os mais simples.
Primeira lei de Kirchhoff
A primeira lei indica que em qualquer nó do circuito, a somatória das correntes elétricas de entrada é equivalente à somatória das correntes de saída do nó. Os nós são simplesmente junções de circuitos que representam pontos onde dois ou mais condutores se encontram, como na gravura.
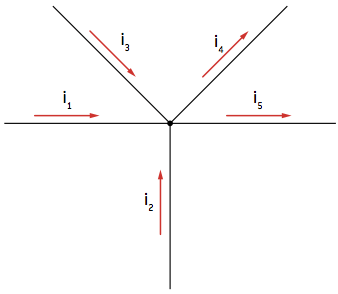
No exemplo ilustrado, há três correntes de entrada na junção – i1, i2 e i3 – e duas correntes deixando o nó – i4 e i5. Aplicando a primeira lei de Kirchoff, temos a seguinte igualdade:
i1 + i2 + i3 = i4 + i5
A primeira lei de Kirchhoff baseia-se no princípio da conservação da carga elétrica. Segundo esse princípio, uma carga elétrica não pode ser criada ou destruída. Assim sendo, Kirchoff deduziu que se um quantidade de corrente com determinada carga elétrica chega a um ponto, essa mesma carga tem de deixar o ponto.
A primeira lei também recebe o nome de “Lei das Correntes” ou “Lei dos Nós”.
Segunda lei de Kirchhoff
A segunda lei envolve malhas, ou seja, circuitos elétricos fechados. A lei determina que sempre que há um percurso fechado, a somatória das diferenças de potencial elétrico será nula. se percorre uma malha fechada em um circuito, a soma algébrica das diferenças de potencial é nula.
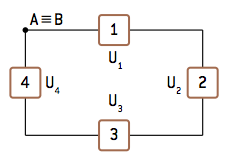
U1 + U2 +U3 – U4 = 0
Exemplo de um circuito com mais de uma malha que não permite simplificação para se tornar de malha única:
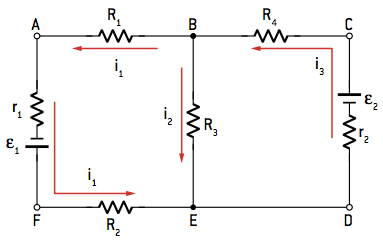
Podemos identificar as malhas ABEFA ou BCDEB ou, ainda, ACDFA.
A segunda lei de Kirchhoff, lei das malhas, é consequência da conservação da energia. Se tivermos uma carga q em um ponto do circuito e o potencial elétrico neste ponto for V, a energia potencial elétrica desta carga será dada por q · V. Considerando que a carga percorra toda a malha do circuito, haverá ganho de energia ao passar pelos geradores e diminuição de energia ao passar por resistores e receptores, no entanto, ao retornar para o mesmo ponto do circuito, sua energia voltará a ser novamente q · V. Concluímos, então, que a variação líquida de potencial é necessariamente nula. Em outras palavras, a diferença de potencial entre um ponto e ele mesmo deve ser zero.
Fique atento. Na hora de analisar uma malha, é importante manter alguns critérios para que não aconteçam equívocos físicos ou matemáticos.
Passo a passo para resolver os exercícios
Segue-se uma sequência de ações que podem ajudar na resolução dos exercícios usando a segunda lei de Kirchhoff.
1. Adote um sentido de corrente na malha.
Se for necessário encontrar a ddp entre os pontos A e B, por exemplo, adote a corrente elétrica neste sentido, ou seja, indo do ponto A para o ponto B. Perceba que é apenas uma referência, não significa que, necessariamente, a corrente faça o percurso desta maneira. Neste caso, o cálculo matemático será útil. Se a corrente resultar em um valor positivo, o sentido adotado está correto; se der negativo, o sentido correto da corrente é de B para A.
2. Formar as ddps dos componentes entre os pontos.
Se o objetivo ainda for encontrar a diferença de potencial entre A e B, ou seja, VA – VB, ao passar por um componente é necessário analisar a diferença de potencial que cada um terá mediante sua função. Para facilitar, adotamos o sinal do potencial de cada elemento como sendo o sinal do potencial que o sentido adotado “encontra” ao chegar, por exemplo:
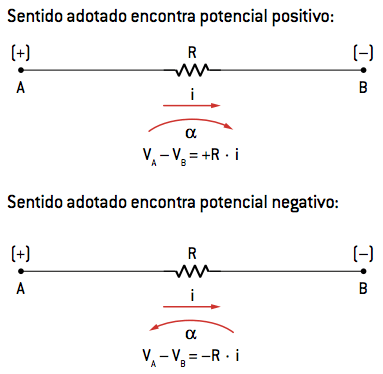
- Para resistências
O sentido natural da corrente para este tipo de componente é sempre do maior (+) potencial para o menor potencial (–). Se o sentido da malha adotado coincidir com o da corrente, o primeiro potencial que a corrente encontrará diante de um resistor será um potencial +. Assim, a ddp para esse resistor é positiva. O contrário também é verdade. Veja: A ddp nos terminais é:
A ddp nos terminais é:VA – VB = +R · i ou VB – VA= –R · i
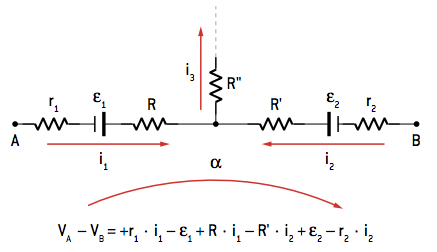
Mediante um sentido adotado para uma malha α, temos:

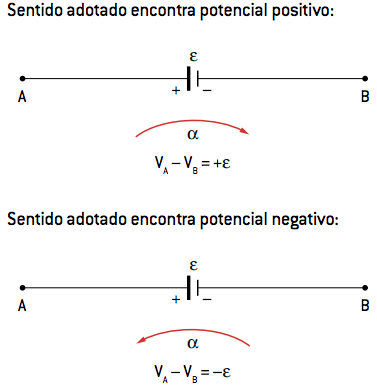
- Gerador ou receptores ideais
Neste caso, a própria representação do elemento carrega informação de qual potencial o sentido da malha adotado está encontrando.
 A ddp nos terminais é:
A ddp nos terminais é:VA – VB = +ε ou VB – VA= –ε
Assim:

Veja o exemplo:
Exercícios
01. Um circuito possui dois resistores, R1 = 5 Ω e R2 = 7,5 Ω, associados em série a duas baterias de resistências internas desprezíveis, ε1 = 100 V e ε2 = 50 V, ligadas uma como gerador e outra como receptor.
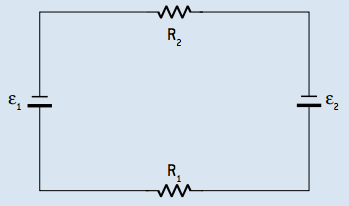
Determine a intensidade da corrente elétrica que percorre esse circuito.
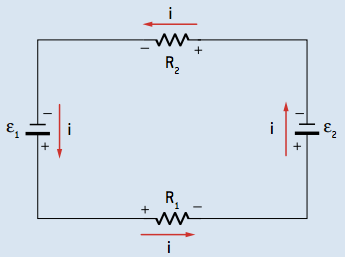
Resolução:
–100 + 5i + 50 + 7,5i = 0
12,5i = 50 ⇒ i = 4
02. Considere o circuito da figura abaixo e determine a intensidade da corrente elétrica indicada pelo amperímetro A, considerando-o ideal.
Dados: ε1 = 90 V; ε2 = 40 V, R1 = 2,5 Ω, R2 = 7,5 Ω e R3 = 5 Ω
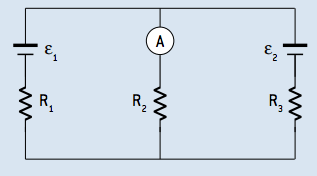
Resolução:
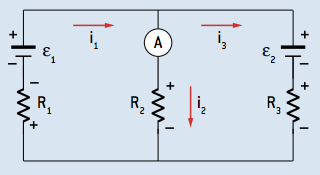
1 = i2 + i3
ΣUmalha = 0
Para a malha esquerda:
7,5 · i2 + 2,5 · i1 – 90 = 0
2,5 · i1 + 7,5 · i2 = 90
Para a malha direita:
40 + 5 · i3 – 7,5 · i2 = 0
5 · i3 – 7,5 · i2 = –40
Resolvendo o sistema:
i1 = 12 A
i2 = 8 A
i3 = 4 A
Por: Wilson Teixeira Moutinho
 A ddp nos terminais é:
A ddp nos terminais é: