Um acontecimento comum no cotidiano que explica o efeito Doppler é a ambulância que percorre as ruas com a sirene ligada. À medida que a ambulância se aproxima de nós, a frequência do som emitido pela sirene parece que aumenta e, à medida que ela se afasta de nós, a frequência do som parece que diminui.
Esse fenômeno é conhecido como efeito Doppler em homenagem ao cientista Christian Doppler que o descreveu no século XIX.
Quando uma fonte sonora e um observador estão em movimento relativo (ambos podem estar em movimento ou apenas um deles), a frequência do som percebida pelo observador, denominada frequência aparente, é diferente da frequência real do som emitido pela fonte. A frequência aparente pode ser maior ou menor que a frequência real, dependendo do afastamento ou da aproximação entre a fonte e o observador.
O efeito Doppler não é uma característica exclusiva das ondas sonoras (mecânicas), pois ele é também observado com as ondas eletromagnéticas.
Para determinar a relação entre a frequência aparente percebida pelo observador e a frequência real do som, vamos considerar, inicialmente, algumas situações particulares.
Fonte sonora em movimento e observador em repouso
Como primeiro caso, considere uma fonte sonora em movimento, com velocidade vf, aproximando-se de um observador em repouso. Nesse caso, haverá um encurtamento aparente do comprimento de onda do som em relação ao normal (fonte parada), conforme mostra a figura.
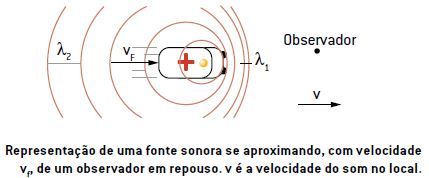
Em virtude do aparente encurtamento do comprimento de onda do som, a frequência aparente (f0) do som percebida pelo observador é maior que a frequência real (fF) da fonte, ou seja, f0 > fF . A relação entre elas é obtida pela equação fundamental da ondulatória (v = λ . f). Assim, temos:
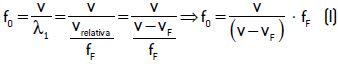
Caso a fonte se afaste do observador, haverá um alongamento aparente do comprimento de onda em relação ao normal, portanto a frequência percebida pelo observador será menor que a frequência real da fonte ( f0 < fF), ou seja:
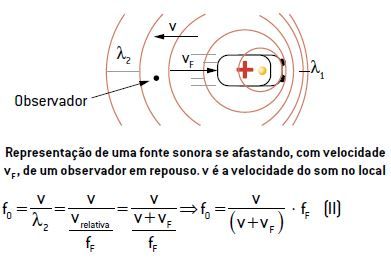
Com base nas equações (I) e (II), podemos estabelecer a relação geral para uma fonte sonora em movimento em relação a um observador em repouso. Combinando as equações, obtemos:
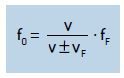
No denominador dessa expressão, o sinal (+) é utilizado para a fonte afastando-se do observador em repouso e o sinal (–) para a fonte aproximando-se do observador.
Fonte sonora em repouso e observador em movimento
Vamos considerar, agora, que um observador em movimento se aproxime de uma fonte sonora em repouso. Para o observador (01), que se aproxima com velocidade v0 da fonte sonora, haverá maior número de encontros com as frentes de ondas do que se estivesse parado, num mesmo intervalo de tempo, conforme mostra a figura.
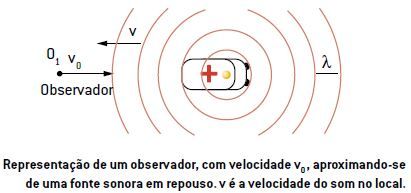
Nesse caso, a frequência aparente (f0) do som percebida pelo observador é maior que a frequência real (fF) da fonte, ou seja, f0 > fF. A relação entre elas é dada por:
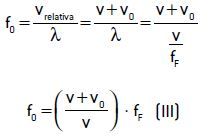
Caso o observador 02 afaste-se da fonte, haverá menor número de encontros com as frentes de onda do que se estivesse parado num mesmo intervalo de tempo. A frequência por ele percebida será menor que a frequência normal (f0 < fF), ou seja:

Com base nas equações (III) e (IV), podemos estabelecer a relação geral entre um observador em movimento e uma fonte sonora em repouso. Combinando as equações, obtemos:
No numerador dessa expressão, o sinal (+) é utilizado para o observador aproximando-se da fonte em repouso, e o sinal (–), para o observador afastando-se da fonte em repouso.
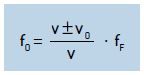
Fonte e observador em movimento
No caso geral, em que tanto a fonte como o observador estão em movimento, a relação entre as frequências percebidas pelo observador (f0) e a real da fonte (fF) é estabelecida combinando-se os dois resultados obtidos nos dois casos particulares anteriores. Assim, obtemos:
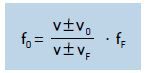
Para a utilização dessa equação, a trajetória deve ser orientada do observador para a fonte, de acordo com a figura:

Autoria: Salete Maria Sabino
Por: Wilson Teixeira Moutinho