Em 1609, o astrônomo e matemático alemão Johannes Kepler, utilizando os dados de observação do dinamarquês Tycho Brahe, desenvolveu e publicou as leis que regem os movimentos dos corpos celestes. Mais tarde, os achados dele ficariam conhecidos como leis de Kepler.
Os dados de Tycho Brahe sobre a órbita de Marte apresentavam alguma discrepância. Kepler tentou usar os dados do colega para ajustar Marte em uma órbita circular em torno do Sol. Contudo, os dados simplesmente não batiam: confiando nos cálculos do colega, Kepler chegou pela primeira vez à conclusão de as órbitas não poderiam ser circulares.
Primeira lei de Kepler: lei das órbitas
Após longos anos de estudo e extensos cálculos matemáticos, Kepler conseguiu ajustar as observações de Marte com a órbita, chegando à conclusão que as órbitas são elípticas e não circulares. Com isso em mente, Kepler formulou a primeira de suas leis:
Todo planeta gira ao redor do Sol em órbita elíptica, na qual o Sol ocupa um dos focos da elipse.
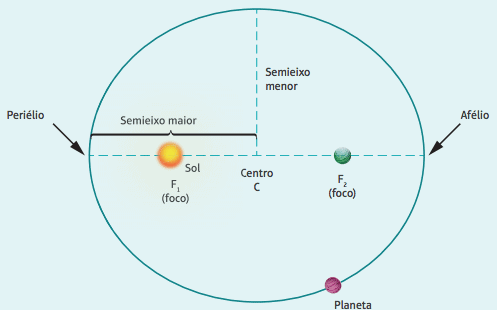
torno do Sol.
Como demonstra o esquema, o ponto de maior proximidade do planeta com o Sol é chamado de periélio; enquanto o ponto mais afastado é o afélio. A distância do periélio ou do afélio define o semieixo maior da elipse.
Explicando melhor: quando a Terra, por exemplo, está no afélio de sua órbita, ela atinge o ponto mais afastado em relação ao Sol. Ao contrário, quando encontra-se no periélio, a Terra atinge o ponto mais próximo em relação ao Sol. A distância entre o Sol, num dos focos dessa elipse, e o centro da elipse é chamada de distância focal.
Observação: a confusão era compreensível, pois apesar das órbitas serem elipses, essas elipses não são muito “achatadas” e se aproximam de uma circunferência. Assim sendo, os focos F1 e F2 são próximos do centro C.
Segunda lei de Kepler: lei das áreas
Ainda analisando os dados sobre Marte, Kepler percebeu um fenômeno ligado à velocidade desse planeta. Quando Marte estava mais próximo do periélio e, com isso, mais próximo ao Sol, o planeta se movia mais rapidamente. À medida que se aproximava do afélio, a velocidade de Marte diminuía. Novos cálculos foram feitos pelo matemático, que acabou formulando a sua segunda lei.
O segmento de reta imaginário que une o planeta ao Sol varre áreas iguais em intervalos de tempo iguais.
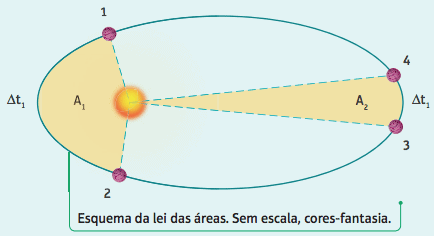
Dessa forma, se um planeta demora o intervalo de tempo Δt1 para ir da posição 1 até a posição 2, determinando uma área A1, e um intervalo de tempo ∆t2 para ir da posição 3 até a posição 4, determinando uma área A2, pela segunda lei de Kepler temos que:
A1 = A2 ⇔ ∆t1 = ∆t2
Explicando – isso significa que as áreas coloridas em bege no esquema são idênticas. Logo o planeta percorre as distâncias entre os pontos 1 e 2 e entre os pontos 3 e 4 no mesmo tempo. Agora, ainda observando o esquema, perceba que a distância linear entre 1 e 2 é várias vezes maior que a distância linear entre 3 e 4. Assim sendo, a velocidade do planeta entre 1 e 2 é muito mais acelerada. A velocidade varia – o planeta acelera em determinados momentos e desacelera em outros – logo:
- quando o planeta vai do afélio para o periélio, seu movimento é acelerado;
- quando o planeta vai do periélio para o afélio, seu movimento é retardado.
Terceira lei de Kepler: lei dos períodos
Após 9 anos de estudos aplicando a primeira e a segunda lei nas órbitas dos planetas do Sistema Solar, Kepler conseguiu relacionar o tempo de revolução (período) do planeta ao redor do Sol à distância média (raio médio) do planeta ao Sol, e isso deu origem à sua terceira lei.
O quadrado do período de translação de um planeta é diretamente proporcional ao cubo do raio médio de sua órbita.
O raio médio ou a distância média do planeta em relação ao Sol pode ser calculado com uma simples média aritmética. Kepler determinou que a média entre a distância do planeta e do Sol no afélio e a mesma distância no periélio, quando divididas por 2, produziam uma distância média do planeta durante a órbita.
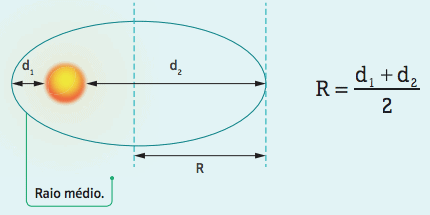
Com esse simples cálculo e mais o T (tempo necessário para o planeta completar uma translação ao redor do Sol (período de translação), a terceira lei pode produzir uma constante:
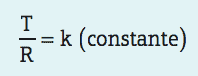
Sabendo determinar essa constante e utilizando o período de translação da Terra – 1 ano – em relação aos demais planetas, Kepler agora era capaz de determinar quando tempo cada planeta demorava para realizar uma volta completa ao redor do Sol.
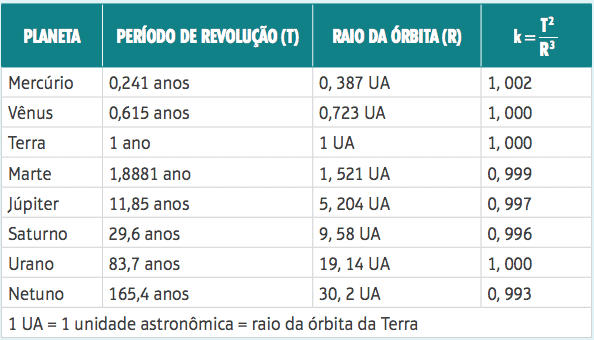
A terceira lei oferece ainda uma “prova“. Quando dividimos o período de translação de cada planeta pelo raio em unidades astronômicas (UA), atingimos um valor próximo a 1. Descartando a margem de erro ao trabalhar com dimensões planetárias, podemos dizer que essa razão é constante – comprovando a teoria de Kepler.
O fato de a razão ser constante permite que a terceira lei de Kepler seja utilizada para descobrir o período ou raio médio de outro planeta ou estrela. As aplicações das 3 leis de Kepler forneciam então a base para o entendimento da relação entre corpos celestes não apenas no Sistema Solar, mas em escala universal.
Mais do que isso, com a constatação de que as órbitas eram elípticas e que os astros desenvolviam trajetórias com variações de velocidade durante seu percurso, Kepler cimentou as bases para que fossem desenvolvidas teorias, no futuro, em relação à gravitação universal.
Exemplo de exercício
O raio médio do planeta Marte é cerca de quatro vezes maior que o raio médio da órbita do planeta Mercúrio. Se o período de revolução Mercúrio é 0,25 anos, qual é o período de revolução Marte?
Resolução
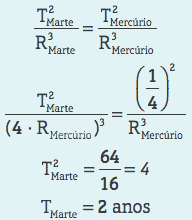
Assim, para os planetas do Sistema Solar, temos:
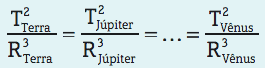
Por fim, podemos dizer que as três leis de Kepler são válidas para quaisquer corpos em órbita de outro corpo, ou seja, podem ser aplicadas em outros sistemas planetários do Universo.
Por: Carlos Artur Matos