O centro de massa é um conceito que falicita muito o estudo do movimento dos corpos rígidos.
Sabe-se que a mecânica é a área da física que estuda o movimento de sua maneira geral. No estudo do movimento existem diferentes corpos. Em várias situações, as dimensões desses corpos não serão levadas em consideração, porém em outras, a informação das dimensões são essenciais.
Uma situação em que as dimensões do corpo são importantíssimas é no estudo da dinâmica do corpo rígido.
Antes de prosseguir é conveniente a definição de corpo rígido. Um corpo rígido é um corpo material constituído de um número de partículas finitas. É importante perceber que no estudo do corpo rígido, por ele possuir muitas partículas, irão aparecer várias equações sendo uma para cada partícula.
A fim de diminuir essa dificuldade, os físicos criaram o conceito de centro de massa. O centro de massa pode ser qualitativamente definido como sendo um ponto do corpo rígido cujo estudo feito através dele é exatamente igual ao estudo da soma de todas as partículas presentes de forma integral.
O centro de massa facilita muito essas equações. A definição matemática do centro de massa se encontra abaixo:
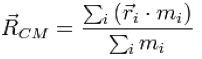
Onde: ri = distância de uma partícula em relação a um referencial
mi = massa de uma partícula
Um exemplo do cálculo do centro de massa pode ser ilustrado abaixo.
 O centro de massa auxilia o cálculo do:
O centro de massa auxilia o cálculo do:
1 – Momento de inércia de um corpo:
O momento de inércia pode ser entendido como sendo a massa de um corpo rígido. Logo se deve substituir a massa pelo momento de inércia quando necessário. Seu cálculo pode ser feito da forma:
Para apenas uma partícula:
Onde: m = massa da partícula
r = distancia da partícula em relação ao um referencial
Para n partículas:
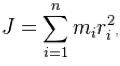
Onde: mi = massa de cada partícula
ri = distância de cada partícula a um referencial
2 – Torque de um corpo rígido:
O torque de um corpo rígido pode ser entendido como sendo uma espécie de segunda lei de Newton para corpos rígidos. Então um cálculo do corpo rígido deve ser feito com o torque e não com a segunda lei de Newton. O torque é equacionado da forma:
Onde: r = vetor posição da partícula
F = força F aplicada na partícula
3 – Momento angular de um corpo rígido:
O momento angular pode ser entendido como sendo a variação do torque, toda vez que o torque varia, haverá a presença do momento angular. O momento angular é calculado da forma:
Para apenas uma particula:
Onde: r = vetor posição da partícula
p = vetor momento linear
Para n partículas:
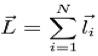
Onde: li = o momento angular de cada partícula.
Por: Luiz Gulherme Rezende Rodrigues
FONTE:
- http://pt.wikipedia.org/wiki/Torque
- http://pt.wikipedia.org/wiki/Momento_angular
- http://pt.wikipedia.org/wiki/Corpo_r%C3%ADgido
- http://pt.wikipedia.org/wiki/Centro_de_massas