Numa colisão mecânica de dois corpos, sempre há trocas de forças internas. Mesmo que haja trocas de forças externas, estas são, normalmente, desprezíveis comparadas com as forças internas. Portanto, numa colisão de dois corpos, as forças externas são desprezíveis e as forças internas do sistema determinam uma resultante nula.
As colisões podem ser consideradas mecanicamente isoladas, ou seja, a quantidade de movimento do sistema de corpos permanece constante antes e depois do choque.
Colisões
Numa superfície plana e horizontal, dois corpos movendo-se com determinada velocidade sofrem uma colisão frontal e central. Nessa colisão, o sistema é considerado mecanicamente isolado tendo em vista que a quantidade de movimento do sistema mantém-se constante.
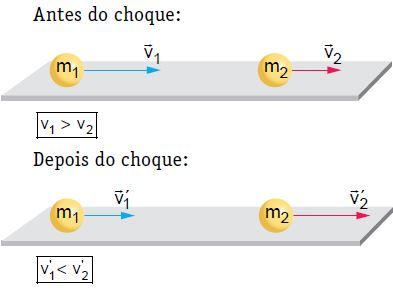
No nosso exemplo, depois do choque, o corpo 2 é impulsionado e tem sua velocidade elevada. Já o corpo 1 pode seguir no mesmo sentido que tinha antes do choque, porém com menor velocidade, parar ou retornar, ou seja, inverter o sentido do seu movimento. Para trabalhar a teoria, consideremos uma das situações, ou seja, aquela em que o corpo 1 segue no mesmo sentido que possuía antes do choque.
Para o sistema formado pelos dois corpos:
Qantes = Qdepois
m1 · v1 + m2 · v2 = m1 · v’1 + m2 · v’2
Para colisões mecânicas unidirecionais (numa única direção), devemos adotar um sentido de orientação para o movimento e usar os sinais v > 0 para velocidade a favor da orientação e v < 0 para velocidade contrária à orientação.
Na equação acima, geralmente não são conhecidas as velocidades v’1 e v’2‘. Portanto, temos uma equação com duas incógnitas. Precisamos de mais uma equação, a do coeficiente de restituição.
Coeficiente de restituição
Para que haja colisão, os corpos 1 e 2, antes do choque, aproximam-se com velocidade relativa vaproximação.
vaproximação = v1 – v2
Depois do choque, os corpos 1 e 2 se afastam com velocidade relativa vafastamento.
vafastamento = v’2 − v’1
O coeficiente de restituição (e) de um choque central e direto é um número adimensional que está associado à energia dissipada na colisão. Ele é obtido pela razão entre os módulos das velocidades de afastamento e aproximação.

Tipos de colisões mecânicas
Como na natureza não é possível criar nem destruir energia, então, numa colisão, a energia mecânica do sistema pode permanecer constante ou diminuir se houver dissipação na forma de calor, deformação e som.
Nessas condições, podemos escrever que a velocidade relativa de afastamento dos corpos, em módulo, é sempre menor ou igual ao módulo da velocidade relativa de aproximação dos corpos.
Colisão inelástica ou perfeitamente inelástica
É o tipo de choque em que, após a colisão, os corpos seguem juntos (com a mesma velocidade). Nesse caso, temos:
vafastamento = 0
v’2 = v’1
e = 0
Na colisão inelástica, a energia cinética do sistema diminui, ou seja, parte da energia mecânica inicial do sistema é transformada em outras formas de energia. Esse tipo de choque é aquele que mais dissipa energia.
Ec após << Ec antes
Colisão parcialmente elástica ou parcialmente inelástica
Nesse choque, depois da colisão, os corpos seguem separados, ou seja, com velocidades diferentes, e o sistema perde uma parte da energia mecânica.
v’2 ≠ v’1
vafastamento ≠ 0
0 < e < 1
Na colisão parcialmente elástica energia cinética do sistema diminui.
Ec após < Ec antes
Colisão perfeitamente elástica ou colisão elástica
Nesse choque, depois da colisão, os corpos seguem separados, ou seja, com velocidades diferentes, e o sistema não perde energia mecânica. Os corpos afastam-se com a mesma velocidade relativa com que se aproximam.
v’2 ≠ v’1
vafastamento = vaproximação
e = 1
Na colisão perfeitamente elástica a energia cinética do sistema permanece constante.
Ec após = Ec antes
Resumo
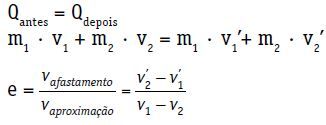
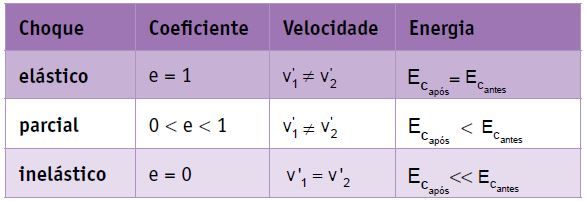
Numa colisão perfeitamente elástica de dois corpos de mesma massa, as velocidades sofrem permutação, ou seja, a velocidade final do corpo 1 é igual à velocidade inicial do corpo 2 e a velocidade final do corpo 2 é igual à inicial do corpo 1
Por: Wilson Teixeira Moutinho
Veja os exercícios resolvidos sobre esse assunto.