Equação de Torricelli

O físico e matemático Evangelista Torricelli (1608-1647) discípulo de Galileu, obteve uma fórmula auxiliar para o movimento uniformemente variado, na qual podemos obter velocidades e deslocamentos sem conhecer, a priori, o tempo de movimento do móvel.

O procedimento para a obtenção da equação de Torricelli é isolar a grandeza tempo na equação horária da velocidade e substituí-la na equação horária da posição. Vejamos como fica:

v = v₀ + a · t → v – v₀ = a · t


 , substituindo esse termo na equação da posição:

Explicando a Equação de Torricelli

Vamos exemplificar como a equação de Torricelli pode ser utilizada. Observe o exercício apresentado abaixo.

Ex: Um móvel se movimenta sobre uma trajetória retilínea partindo da posição s₀ = 40 m, com velocidade inicial de v₀ = –20 m/s e aceleração constante a = +5 m/s², calcularemos a velocidade escalar instantânea do móvel ao passar pela posição s = 10 m de sua trajetória.

Observe que, a priori, não conhecemos o tempo gasto para atingir essa posição. Sabemos que ele poderia ser calculado.

Utilizando a equação de Torricelli, temos:

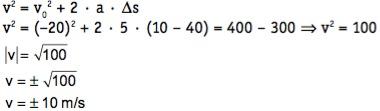
Então, do ponto de vista matemático temos duas soluções para o problema: v₁ = 10 m/s ou v₂ = –10 m/s. Do ponto de vista físico, precisamos avaliar se as soluções matemáticas encontradas satisfazem as condições físicas do problema. Construiremos uma representação da trajetória para verificarmos quantas vezes e em qual sentido o móvel passa pela posição 10 m.

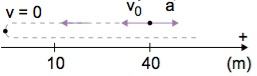
Como a aceleração é contrária à velocidade inicial, ela vai retardar o movimento do móvel até parar e depois acelera-o de volta. Portanto, o móvel passa duas vezes pela posição 10 m, uma na ida (–10 m/s) e outra na volta (+10 m/s).

v = ±10 m/s

Agora, se quisermos saber a velocidade do móvel ao passar pelo espaço 90 m, teremos:

v² = v₀ ² + 2·a· (s – s₀)
v² = (–20)² + 2 · 5 ·(90 – 40)
v² = 400 + 500
v² = 900

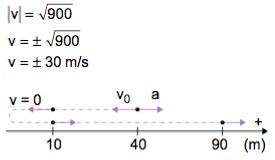
O móvel passa uma única vez pela posição 90 m e a favor da orientação da trajetória. Portanto:

v = +30 m/s

Exercício Resolvido

Uma partícula subatômica, deslocando-se com velocidade constante igual a 6 · 10⁶ m/s, penetra numa região de campo elétrico uniforme e sofre uma desaceleração constante de 1,2 · 10¹⁴ m/s². A distância percorrida, em centímetros, pela partícula até parar é:

a)  15
b)  20
c)  25
d)  35
e)  30

Resposta: A
Velocidade inicial: v₀ = 6 · 10⁶ m/s.
Desaceleração: a = –1,2 · 10¹⁴ m/s (movimento retardado)
Velocidade final: v = 0

Pela equação de Torricelli:

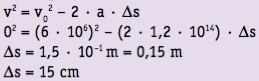
Por: Wilson Teixeira Moutinho