Em física, o equilíbrio ocorre quando as forças que atuam num corpo tendem a uma resultante nula. E, quando esse equilíbrio faz com que o corpo, ao menos em relação ao meio que estudamos, permaneça em repouso, estamos lidando com o equilíbrio estático de um corpo.
O estudo do equilíbrio estático é possível de duas maneiras: analisando o equilíbrio num ponto material (tamanho do corpo desprezível) e analisando-o num corpo extenso (tamanho do corpo não desprezível).
Ponto material e corpo extenso
A parte da física que estuda as condições para que um ponto material ou um corpo extenso permaneça em equilíbrio é a estática. Em outras palavras, é um ramo da mecânica que se concentra em compreender a combinação de forças capaz de se anular, fazendo com que um corpo permaneça “parado”.
A diferença do estudo do equilíbrio estático de um ponto material e de um corpo extenso está no movimento de rotação. No ponto material, desprezível em dimensões, todas as forças necessariamente atuam a partir ou contra um mesmo ponto – não há movimento de rotação ou deslocamento do corpo com a atuação das forças. Quando um corpo extenso, contudo, é submetido a essas mesmas forças, ele pode realizar movimentos de rotação.
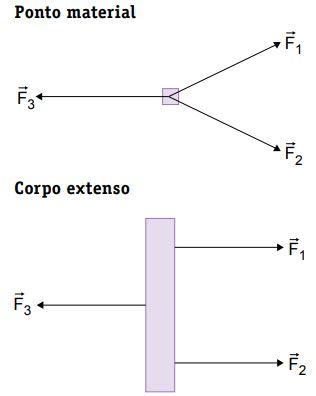
Equilíbrio de um ponto material
Um corpo é considerado ponto material quando pudermos desprezar o seu tamanho. O ponto material, em termos “reais”, não existe. Contudo, o ensaio em um sistema que despreza dimensões e massa do corpo é útil para que matemáticos e físicos compreendam como as forças operam entre si e em relação a determinado ponto de atuação. Em termos reais, esse tipo de análise pode ser feita quando todas as forças atuam no mesmo ponto de um corpo de prova, replicando o comportamento do ponto material.
A condição de equilíbrio de ponto material é que ele não realize movimento de translação, ou seja, a resultante das forças aplicadas deve ser igual a zero.
Equilíbrio de um ponto material ⇒ Resultante das forças igual a zero
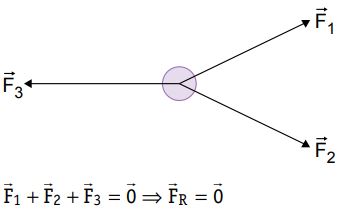
Nas aplicações do equilíbrio de um ponto material, podemos relacionar as forças aplicadas pelos métodos da decomposição ou da poligonal. O que isso quer dizer? Bem, se todas as forças atuam a partir de uma mesma reta, ou seja, uma mesma direção, ainda que em sentidos opostos, basta que somemos todas as forças que seguem para um dos sentidos, subtraindo aquelas que atuam no sentido oposto.
Por outro lado, quando há ângulos diferentes entre as forças, primeiro precisamos projetar a incidência de cada uma delas sobre uma mesma reta – para somente então realizar a resultante entre as forças que atuam em sentidos opostos.
Equilíbrio de um corpo extenso
Um ponto material estará em equilíbrio quando a resultante das forças for igual a zero. Esse equilíbrio é o de translação. Corpos extensos sobre a atuação de forças podem gerar basicamente dois tipos de movimentos: rotação e translação. Assim sendo, a análise do equilíbrio precisa ocorrer em duas frentes:
- Equilíbrio de translação: ocorre quando a resultante das forças aplicadas nesse corpo é igual a zero, ou seja, a soma vetorial de todas as forças aplicadas no corpo deve dar resultante nula. De certo modo, essa soma é muito similar ao que ocorre quando avaliamos a resultante sobre o ponto material – só que desta vez, há distâncias entre os pontos de aplicação das forças que devem ser consideradas.
- Equilíbrio de rotação: ocorre quando o momento resultante é igual a zero, ou seja, a soma dos momentos de todas as forças aplicadas no corpo deve ser nula. O momento da força é uma simples multiplicação entre a força e a distância do ponto de aplicação da força (F . d).
Por exemplo: a figura mostra uma barra horizontal apoiada num suporte de maneira que ela possa girar. Nos seus extremos estão apoiados dois corpos de massa m1 e m2 .
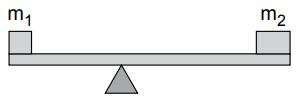
As forças aplicadas no sistema barra e blocos são:
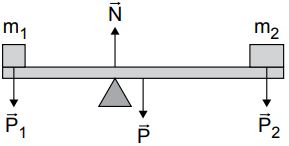
Estando o sistema em equilíbrio de translação, bastante similar ao que calculamos para o ponto material, temos:
FR = 0 ⇒ N = P + P1 + P2
Contudo, como lidamos com um corpo no qual várias formas atuam em partes distintas desse objeto, precisamos colocar também o sistema em equilíbrio de rotação, e assim temos:
MR = 0 ⇒ MN + MP1 + MP2 + MP = 0
Exercícios Resolvidos
1. Um ponto material recebe a ação de três forças, conforme indicação na figura abaixo. Calcule a intensidade da força de tração T1 e T2 .
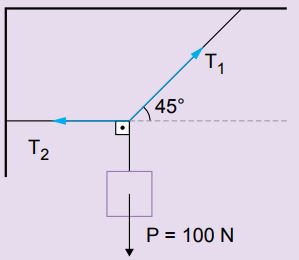
Resposta: As trações podem ser encontradas pelo método da poligonal e da decomposição.

2. Um corpo está suspenso por meio de dois fios, como mostra a figura a seguir. Sabendo-se que as forças de tração exercidas pelos fios são de intensidades iguais, calcule a intensidade delas.
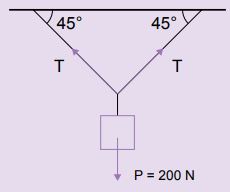
Resposta: O ângulo formado entre os dois fios que sustentam o corpo é de 90°.
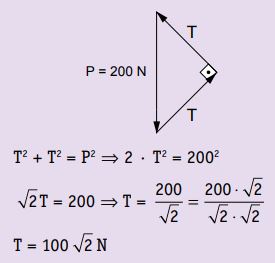
3. Conhecendo as trações nos fios que sustentam o bloco da figura abaixo, calcule a intensidade da força peso do bloco. Considere o sistema em equilíbrio.
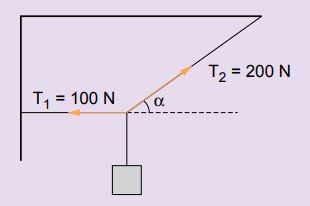
Resposta: Estando o sistema em equilíbrio, a resultante das forças aplicadas no corpo é nula.

4. Uma barra de peso 600 N está apoiada em dois suportes que a mantêm em equilíbrio horizontal. Calcule a intensidade das forças aplicadas pelos apoios na barra.
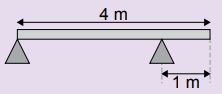
Resposta: Vamos marcar as forças aplicadas na barra.
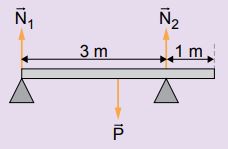
Colocando o polo das forças em N1 , temos:
MR = 0
MP + MN2 = 0
P · dP – N2 · d2 = 0
600 · 2 – N2 · 3 = 0
3 · N2 = 1.200
N2 = 400 N
FR = 0
N1 + N2 = P
N1 + 400 = 600
N1 = 200 N
Por: Carlos Artur Matos