Um pêndulo simples consiste de um fio leve e inextensível de comprimento L, tendo na extremidade inferior, por exemplo, uma esfera de massa m; a extremidade superior é fixada em um ponto, tal que ele possa oscilar livremente (resistência do ar desprezível), com amplitudes pequenas (
máximo = 15o) (fig.1).
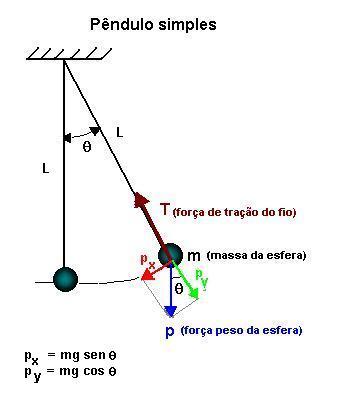
Quando o pêndulo é deslocado de sua posição de equilíbrio, ele oscila sob a ação da força peso, apresentando um movimento periódico. As forças que atuam sobre a esfera de massa m são: a força peso p e a força de tração T.
A força centrípeta, Fc, que mantém o pêndulo na trajetória de um arco circular, é a resultante da força de tração T que o fio exerce e da componente da força peso py na direção do raio, que imprime a aceleração centrípeta, ac:
ac = V2 / R
Podemos determinar a aceleração da gravidade local, medindo a aceleração tangencial e o ângulo de um pêndulo simples.
g = – a t / sen
Período do pêndulo simples
Quando o ângulo for muito pequeno ( aproximadamente 3o) 
sen aproximadamente igual a . Neste caso o pêndulo executa um movimento harmônico simples (MHS) e o período pode ser calculado pela expressão:
T = 2
(L / g )1/2
Período, frequência, e velocidade angular de um pêndulo simples
O período de um pêndulo, T, é o tempo que ele leva para dar uma oscilação completa, ou seja, o tempo que leva para sair da sua posição inicial e voltar para a mesma posição. Para medir este tempo vamos medir o tempo 
t que leva para dar um número determinado de oscilações, n:
qT = t / n
A frequência é o número de oscilações, n, que o pêndulo executa em uma unidade de tempo, t.
Procedimento Experimental
- Faça o pêndulo oscilar em um plano paralelo a régua.
- Observe como fica o enquadramento do movimento com o padrão de medida.
- Faça as medições conforme estipula o procedimento a seguir:
Deixe o pêndulo oscilar dez vezes cronometrando o tempo e meça o período do pêndulo, Utilizando os ângulos dados na apostila, utilizando a formula T = 2 (L / g )1/2 encontre o comprimento do fio. Utilizando a outra medida de L agora conhecida encontre o período e através da mesma formula obtenha o valor da aceleração da gravidade.
Conclusão
A partir do experimento realizado com o pendulo simples, em condições ideais, (sem a interferência de forças externas) podemos verificar que a aceleração da gravidade atua em toda parte e preserva suas características básicas onde quer que aplicadas.
Autoria: Alex Zenon
