Trabalho (Física)

Geralmente, associamos a palavra “trabalho” a um esforço relacionado a qualquer atividade física ou mental. Em física, no entanto, o termo “trabalho” está associado à alteração da energia de um corpo

Trabalho, portanto,  é uma grandeza física escalar associada à ação de uma força ao longo do deslocamento realizado por um corpo. Esse esforço exercido sobre o corpo altera sua energia e tem relação direta com o produto da força que causa o esforço pela distância percorrida pelo corpo, considerada durante a ação dessa força, que pode ser constante ou variável.

1. Trabalho de uma força constante

Suponha que um móvel, ao longo de um deslocamento de módulo d, sofra a ação de uma força constante de intensidade F, inclinada de θ em relação à direção do deslocamento.

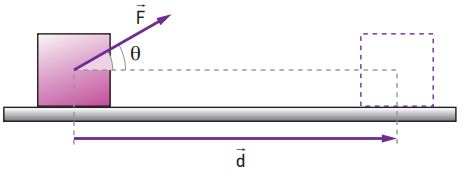
Por definição, o trabalho (T) realizado pela força F constante, ao longo do deslocamento d, é dado por:

T = F · d · cos θ

Nessa expressão, F é o módulo da força, d é o módulo do deslocamento e θ, o ângulo formado entre os vetores F e d. No Sistema Internacional (SI), a unidade de força é o Newton (N), a unidade de deslocamento é o metro (m) e a unidade de trabalho é o joule (J).

Dependendo do ângulo θ entre os vetores F e d, o trabalho realizado por uma força pode ser positivo, nulo ou negativo, de acordo com as características descritas a seguir.

1. Se θ é igual a 0° (força e deslocamento têm mesmo sentido), temos que cos θ = 1. Nessas condições:

T = F · d

2. Se 0° ≤ θ < 90°, temos que cos θ > 0. Nessas condições, o trabalho é positivo (T > 0) e recebe a denominação de trabalho motor.

3. Se θ = 90°, temos que cos θ = 0. Nessas condições, o trabalho é nulo (T = 0), ou a força não realiza trabalho.

4. Se 90° < θ ≤ 180°, temos que cos θ < 0. Nessas condições, o trabalho é negativo (T < 0) e recebe a denominação de trabalho resistente.

5. Se θ é igual a 180° (força e deslocamento têm sentidos opostos), temos que cos θ = –1. Nessas condições:

T = –F · d

Note que o trabalho:

• é sempre de uma força;
• depende de uma força e de um deslocamento;
• é positivo quando a força favorece o deslocamento;
• é negativo quando a força se opõe ao deslocamento;
• seu módulo é máximo quando o ângulo entre o vetor deslocamento e o vetor força é 0° ou 180°.
• seu módulo é mínimo quando a força e o deslocamento são perpendiculares entre si.

2. Trabalho de uma força variável

No item anterior, para calcular o trabalho de uma força constante, utilizamos a equação T = F · d · cos θ. No entanto, existe outra maneira de calcular esse trabalho, utilizando, para isso, o método gráfico. A seguir, temos o gráfico de uma força F constante em função do deslocamento produzido.

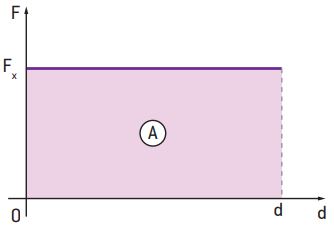
Observe que a área A do retângulo indicado na figura é dada por A = F_X · d, ou seja, o trabalho é numericamente igual à área da figura formada pela curva (linha do gráfico) com o eixo do deslocamento, no intervalo considerado. Assim, escrevemos:

T = Área

Podemos aplicar essa propriedade gráfica no caso de uma força de módulo variável para calcular o trabalho realizado por essa força. Considere que a força F varie em função do deslocamento, conforme mostra o gráfico seguinte.

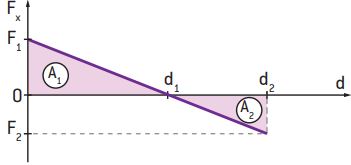
A área indicada por A₁ fornece o trabalho da força F no deslocamento (d₁ – 0), e a área indicada por A₂ fornece o trabalho da força F no deslocamento (d₂ – d1). Como a área A₂ se encontra abaixo do eixo do deslocamento, o trabalho da força, nesse caso, é negativo. Assim, o trabalho total da força F, no deslocamento de 0 a d₂, é dado pela diferença entre a área A₁ e a área A₂.

T = A1 – A2

Observação
Cuidado para não utilizar o sinal de menos duas vezes. Uma dica para resolver essa situação é calcular as duas áreas em módulo e, depois, fazer a diferença entre a área acima do eixo d e a área abaixo do eixo d.

3. Trabalho resultante ou total

Os objetos em estudo (partículas, blocos etc.) podem estar sujeitos a um conjunto de forças que atuam simultaneamente durante um determinado deslocamento. Como exemplo, considere a figura a seguir, que mostra um bloco sob a ação de quatro forças constantes, F₁, F₂, F₃ e F₄, durante um deslocamento d.

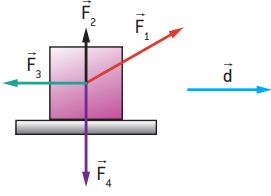
O trabalho resultante da ação simultânea das quatro forças pode ser obtido de dois modos, descritos a seguir.

1. Calculamos o trabalho de cada força individualmente (não esquecendo o sinal) e efetuamos a soma algébrica de todos os trabalhos:

T_R = T₁ + T₂ + T₃ + T₄

2. Calculamos a força resultante e aplicamos a definição de trabalho:

T_R = F_R · d · cos θ

Observação
Se existirem forças de módulos variáveis, utilizaremos, exclusivamente, o primeiro modo (soma algébrica).

4. Exercício de exemplo

Um bloco desliza em um plano inclinado de 37° com a horizontal sob a ação de três forças, conforme mostra a figura a seguir.

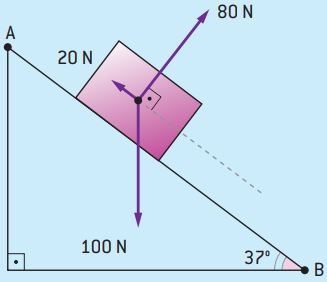
Considerando sen 37° = cos 53° = 0,60 e cos 37° = = sen 53° = 0,80, determine o trabalho de cada uma das forças no deslocamento AB, de 10 m, e o trabalho resultante sobre o corpo.

Resolução

Sendo T = F · d · cos θ, temos:

• Para a força de 100 N, o ângulo θ entre a força e o deslocamento AB é de 53° (90° – 37°):
  T₁₀₀ = F · d_AB · cos 53°
  T₁₀₀ = 100 · 10 · 0,60
  T₁₀₀ = 600 J (motor)
• Para a força de 80 N, o ângulo θ entre a força e o deslocamento AB é de 90°:
  T₈₀ = F · d_AB · cos 90°
  T₈₀ = 80 · 10 · 0
  T₈₀ = 0 J (nulo)
• Para a força de 20 N, o ângulo θ entre a força e o deslocamento AB é 180°:
  T₂₀ = F · d_AB · cos 180°
  T₂₀ = 20 · 10 · (–1)
  T₂₀ = –200 J (resistente)
• O trabalho resultante será a soma algébrica de todos os trabalhos:
  T_R = T₁₀₀ + T₈₀ + T₂₀
  T_R = 600 + 0 – 200
  T_R = 400 J

Por: Daniel Alex Ramos

Veja também:

• Energia Cinética, Potencial e Mecânica