Esta demonstração é encontrada na maioria dos livros de física em três volumes, mas raramente nos livros de volume único. Para aqueles que gostam aí vai.
Para a demonstração da equação de Gauss, vamos considerar um espelho esférico que obedece às condições de Gauss, ou seja, os raios luminosos envolvidos estão pouco inclinados e pouco afastados em relação ao eixo principal.
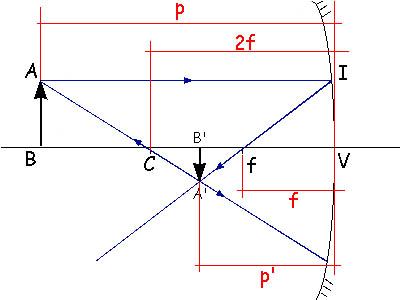
Construção da imagem de um objeto real, que se encontra atrás do centro de curvatura.
Se estamos obedecendo as condições de Gauss, o comprimento do segmento AB é muito próximo ao do segmento IV:
Observe que fV = f e CV = 2f e que os triângulos ABC e A’B’C’ são semelhantes como pode ser observado na figura abaixo.
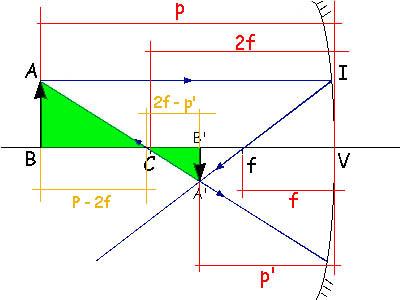
Os triângulos sublinhados são semelhantes.
Então vale a seguinte relação matemática
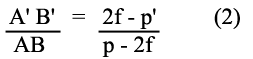
Os triângulos A’B’f e IVf também são semelhantes, como está destacado na figura abaixo.
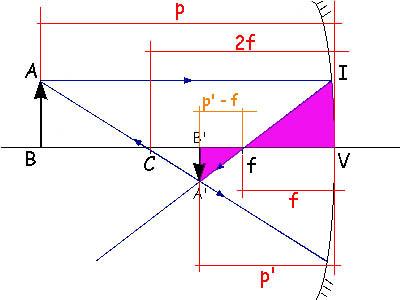
Os triângulos sublinhados são semelhantes.
Então vale a seguinte relação matemática
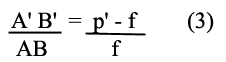
Considerando a aproximação da relação (1), podemos considerar a equação (2) = (3), então teremos:
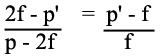
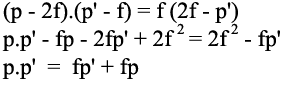
Nesta passagem fiz a multiplicação em cruz e desenvolvi os produtos
Se dividirmos ambos os membros por pp’f, teremos:
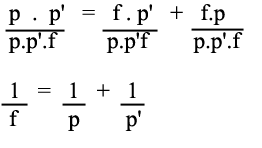
Que é a equação dos pontos conjugados de Gauss.
Autoria: Ricardo Forner