O físico alemão Werner Heisenberg (1901-1976) postulou, em 1927, o princípio da incerteza, o qual estabelece que, na teoria quântica, a incerteza é inerente às próprias condições iniciais, como afirma o enunciado a seguir.
É impossível medir, no mesmo instante, com precisão ilimitada, a posição e a quantidade de movimento de uma partícula e, consequentemente, sua velocidade.
A física clássica de Newton é caracterizada pela precisão e pelo determinismo: “Se conhecermos as condições iniciais de uma partícula macroscópica e as forças que atuam sobre ela, certamente poderemos prever suas condições em qualquer instante posterior”.
Porém, no mundo microscópico, as partículas podem se comportar como ondas e aprendemos, em ondulatória, que uma onda não apresenta uma posição muito bem definida. Foi estudando esse assunto que Heisenberg postulou o seu princípio.
Exemplificando o princípio da incerteza
Para entender melhor a imprecisão de medidas no mundo quântico, compare duas situações distintas do mundo clássico.
Na primeira, pode-se perceber que um corpo está quente somente olhando para ele e detectando algumas das características que os corpos apresentam em altas temperaturas, por exemplo, sabe-se que uma quantidade de água, ao nível do mar, está à temperatura próxima de 100 °C somente pelo vapor que se desprende dela. Neste caso, o ato de observar pode ser chamado de não interação com o sistema ou, simplesmente, pode-se dizer que o observador da temperatura da água não interagiu com ela.
Em um segundo caso, se fosse usado um termômetro massivo para medir a temperatura de uma pequena quantidade de água fervente, o simples contato entre o termômetro e a água poderia afetar a temperatura medida. De fato, os corpos em contato tendem ao equilíbrio térmico e, por meio dessa transferência de energia da água para o líquido no interior do termômetro, ocorre a dilatação térmica deste, o que possibilita a leitura na escala de temperatura. No mundo macroscópico, essas variações podem ser previstas e corrigidas.
Já as incertezas do mundo quântico não são da mesma natureza que as do mundo macroscópico, em decorrência da própria natureza ondulatória que se observa em quântica.
Uma onda não pode ser confinada em um ponto, por isso muitos experimentos, no contexto da física quântica, têm demonstrado que o ato de medir um sistema tão pequeno impõe às medidas uma imprecisão mínima, relacionada diretamente à constante de Planck. Ao admitir o elétron como onda, deve-se admitir, em decorrência, que uma onda se estende ao longo de, pelo menos, uma direção e, em um intervalo mínimo de medida, qualquer ponto ao longo desse elétron pode evidenciar sua presença.
Deve-se destacar, portanto, que o princípio da incerteza é uma característica do mundo quântico. Assim, a ideia de elétrons como bolinhas deve ser reformulada. Segundo o físico estadunidense Richard Feynmann (1918-1988), “os elétrons devem ser tratados estatisticamente, pela densidade de probabilidade associada à onda de matéria”.
Formulação do princípio da incerteza de Heisenberg
Heisenberg estabeleceu que a incerteza da posição e a quantidade de movimento são inversamente proporcionais, ou seja, quanto maior for a precisão na medida da posição, menor será a precisão na medida da quantidade de movimento ou da velocidade.
Ele afirmou também que o produto da incerteza da posição pela quantidade de movimento nunca será menor que a razão entre a constante de Planck e 4π. Com isso, podemos perceber que, mesmo com os melhores instrumentos de medida e com a tecnologia mais avançada possível, sempre existirá um limite para a precisão das medidas obtidas.
Matematicamente, podemos escrever as conclusões de Heinsenberg de acordo com a equação a seguir.
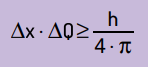
Em que:
- Δx é a incerteza sobre a posição da partícula;
- ΔQ é a incerteza sobre a quantidade de movimento da partícula, que pode ser calculada efetuando-se a multiplicação da massa pela variação da velocidade (ΔQ = m · Δv). Em muitos enunciados, a variação da quantidade de movimento é chamada de momento e é representada por Δp;
- h é a constante de Planck (h = 6,63 · 10–34 J · s).
No curso superior é muito comum essa equação ser escrita como:

Exercício resolvido
01. A medida da velocidade de um elétron, em um experimento, foi de 2,0 · 106 m/s, com precisão de 0,5%. Qual é a incerteza na posição medida para esse elétron, sendo sua massa 9,1 · 10–31 kg?
Adote π = 3,14.
Resolução
Calculando a quantidade de movimento do elétron e sua respectiva incerteza, temos:
Q = m · v = 9,1 · 10–31 · 2 · 106
Q = 1,82 · 10–24 kg · m/s
Como a quantidade de movimento é diretamente proporcional à velocidade, elas terão a mesma precisão de 0,5%.
ΔQ = 0,5% · 1,82 · 10–24
ΔQ = 0,5 / 100 · 1,82 · 10–24 = 5 · 10–5 · 1,82 · 10–26
ΔQ = 9,1 · 10–27 kg · m/s
Essa é a incerteza da quantidade de movimento. Aplicando o princípio da incerteza para a localização do elétron, temos:
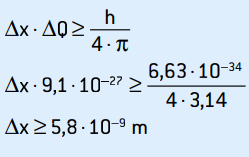
Essa é a incerteza da posição do elétron, que corresponde a cerca de 58 diâmetros atômicos.
A incerteza da posição também pode ser calculada em porcentagem:
Δx ≥ 5,8 · 10–9 · 100%
Δx ≥ 0,000 000 58%
Por: Daniel Alex Ramos