O engenheiro francês Sadi Carnot, ainda no ano de 1824, desenvolveu um amplo estudo na área da termodinâmica, desenvolvendo um ciclo “ideal“. O objetivo de seus estudos sobre a forma com que o calor se transformava visava aumentar a eficiência e o rendimento de máquinas.
Carnot concluiu que uma máquina precisa receber calor de uma fonte (QQ) e que troque o mínimo possível de calor com a fonte fria (QF). Quanto menor for essa troca, maior será o trabalho T resultante do ciclo (T = QQ – QF). Ou seja, o processo terá melhor rendimento.
Carnot idealizou um ciclo teórico de rendimento máximo realizado em quatro etapas distintas. Esse ciclo de rendimento máximo é denominado Ciclo de Carnot.
Considere uma máquina térmica como a proposta na figura a seguir. A fonte de calor opera em uma temperatura determinada TQ na máquina, que é exposta também a uma fonte fria de temperatura TF. A máquina retira uma quantidade de calor QQ da fonte quente, realiza um trabalho T e rejeita um calor QF para a fonte fria.
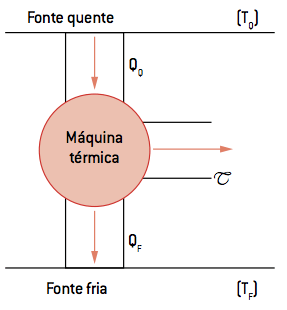
As 4 etapas do Ciclo de de Carnot
O Ciclo de Carnot considera que a configuração ideal do processo deve obedecer a quatro transformações térmicas distintas – duas adiabática e duas isotérmicas. Para referência, nas transformações isotérmicas o gás envolvido na transformação sofre mudanças de pressão e volume, porém mantém constante a sua temperatura. Na transformação adiabática, não há troca de calor com o ambiente, ou seja, o sistema está isolado de trocas externas de calor.
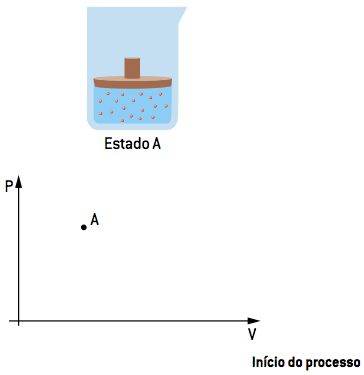
No processo exemplificado a seguir, imaginamos um estado inicial A para o gás em questão – ao qual iremos impor o Ciclo de Carnot.
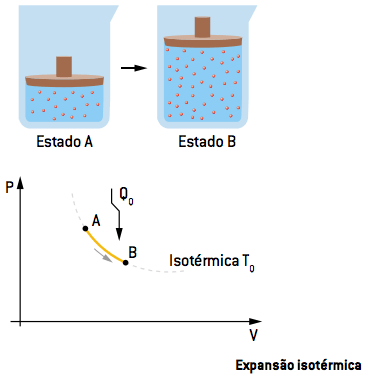
I. Expansão isotérmica AB
Na primeira etapa, o gás sofre uma expansão isotérmica (temperatura constante) até um estado B, recebendo, para isso, calor da fonte quente QQ. No gráfico, é possível verificar que ao receber maior calor da fonte, o gás expande, aumentando seu volume, ao mesmo tempo em que alivia a pressão.
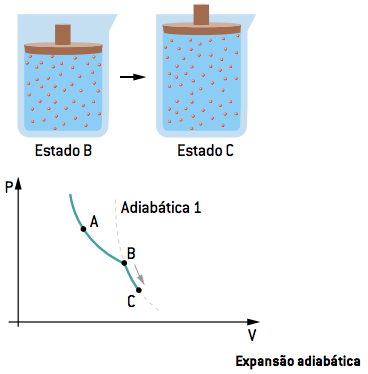
II. Expansão adiabática BC
Na segunda etapa, interrompe-se o contato com as fontes. O gás sofre uma expansão adiabática do estado B até o estado C. A velocidade de ganho de volume reduz, assim como a queda de pressão.
III. Compressão isotérmica CD
Na terceira etapa, o gás sofre uma compressão isotérmica até um estado D, rejeitando certa quantidade de calor para a fonte fria QF. Ou seja, ao perder temperatura, o gás se comprime e a pressão volta a aumentar (como visto na ilustração, com a maior pressão do êmbolo).
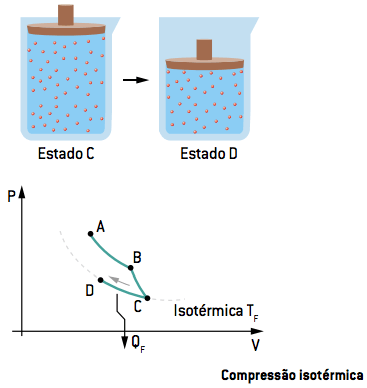
IV. Compressão adiabática DA
Na quarta etapa, interrompe-se novamente o contato com as fontes. O gás continua a ceder à pressão e reduz um pouco mais o seu volume, até retornar ao estado inicial A, onde pode realizar novamente o ciclo de forma contínua.
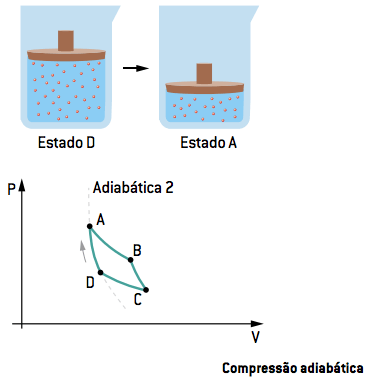
Em resumo, o ciclo de Carnot, que representa uma máquina térmica em rendimento máximo, consta de duas transformações adiabáticas alternadas e duas isotérmicas. O ciclo poderia, em teoria, manter o trabalho de forma contínua, sempre retornando ao estado inicial A após a realização do trabalho.

Fórmula
Carnot demonstrou que, se fosse possível construir uma máquina com essas características (uma espécie de moto-contínuo), ela teria o máximo de rendimento. A cada novo ciclo, a quantidade de calor trocada entre as fontes acabariam sendo proporcionais às temperaturas absolutas dessas fontes, mantendo o ciclo por um tempo indefinido.
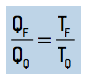
Substituindo essa relação na equação do rendimento, teríamos que:
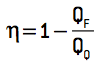
obtemos:
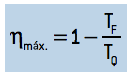
Esse é o máximo rendimento teórico possível para uma máquina térmica que funcione em ciclos. Como toda máquina teórica e ideal, o experimento funciona como base para comparação e mensuração em máquinas executáveis. Em outras palavras, nenhuma máquina térmica real pode atingir esse valor de rendimento.
Observação
Para aumentar o rendimento de uma máquina térmica ideal, a razão TF/TQ deveria ser a menor possível. Em outras palavras, como as temperaturas para fins de cálculo sempre são usadas em Kelvin, uma máquina cuja fonte fria operasse no zero absoluto atingiria uma razão tendendo a zero. Nesse caso, o rendimento seria de 100%.
Exercício Resolvido
O gás perfeito contido em uma máquina térmica retira 4000 J de calor da fonte quente e rejeita 3000 J para a fonte fria em cada ciclo. A temperatura da fonte fria é 27 °C e a da fonte quente é 227 °C. Determine para cada ciclo:
- o trabalho realizado;
- o rendimento da máquina;
- o rendimento máximo teórico da máquina
Resolução:
1. O trabalho realizado pode ser calculado pela expressão:
T = QQ – QF
T = 4000 – 3000 ⇒ T = 1000 J
2. O rendimento da máquina pode ser assim obtido:
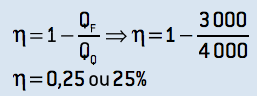
3. Para obter o rendimento teórico máximo, é necessário que essa máquina opere em um ciclo de Carnot, cujo rendimento pode ser calculado:
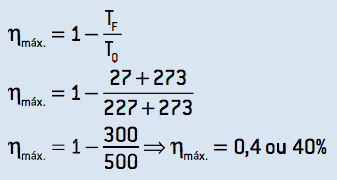
Comparando os resultados dos itens B e C, podemos afirmar que a máquina não opera em um ciclo de Carnot e é uma máquina viável.
Por: Carlos Artur Matos