Um dos brinquedos mais procurados em qualquer parque de diversões é a montanha-russa. Com capacidade para cerca de 24 pessoas, são mais de 600 sextilhões de combinações possíveis para dispor os usuários, com uma simples permutação entre 24 lugares.
Permutação simples
Em um carro, além do motorista, podem ser transportados mais quatro passageiros: um no banco do carona, o famoso “lugar da frente”, e, no banco detrás, têm-se a posição da janela à esquerda, a posição central e a da janela à direita. De quantas maneiras diferentes podem ser dispostos quatro passageiros, não considerando o motorista, nas acomodações desse carro?
Analisadas inicialmente as possibilidades para o banco do carona, conclui-se que existem quatro. Fixando um passageiro nessa posição, restam três que poderão se acomodar, por exemplo, no banco de trás ao lado da janela da esquerda. Seguindo essa ideia, ou seja, fixando mais um passageiro nessa posição, restarão dois, que poderão, por exemplo, se acomodar no banco de trás, no centro. Fixando mais um, restará apenas um, que com certeza deverá se sentar no banco de trás na posição da janela da direita.
Pelo princípio multiplicativo, tem-se que o total de possibilidades é dado por 4 · 3 · 2 · 1 = 24 posições distintas no carro, desconsiderando o motorista. Cada uma das disposições tomadas é uma permutação simples dos lugares possíveis no carro.
Note que o total de permutações simples foi calculado aplicando-se o princípio multiplicativo que remeteu à notação de fatorial. Dessa forma:
Exemplo:
O presidente de uma grande empresa reserva todas as segundas-feiras de manhã para realizar uma reunião com todos os diretores. Considerando que existem cinco diretores nas mais diversas áreas dessa empresa, calcule de quantas maneiras essas seis pessoas (presidente e diretores) podem ser dispostos numa mesa não redonda. Esse é um típico caso de permutação simples. Para isso, basta calcular
P6 = 6.5.4.3.2.1 = 720
Ou seja, o presidente e os diretores podem ser dispostos em uma mesa não redonda de 720 maneiras distintas.
Permutação com repetições
Verão, sol, calor. Não podia ser diferente: a família Shroder foi para o litoral e decidiu ficar lá seis dias. Embora a principal atividade fosse a praia, a família escolheu quatro atrações para se entreter no período da noite. São elas: cinema, feira de artes, sorveteria e parque de diversões. Como a família não gosta de ficar em casa, resolveu que iria duas vezes em duas das atrações. Depois de muito discutirem, escolheram o cinema e a feira de artes.
De quantas maneiras distintas pode ser feito o programa da família Shroder nesses seis dias?
Observe que, embora a família tenha saído seis vezes, o total de possibilidades será menor que 6, já que duas delas se repetem duas vezes cada. Nesse caso, não se trata mais de uma permutação simples.
Por exemplo, se as duas idas ao cinema fossem eventos distintos, isso resultaria em 2! novas possibilidades apenas pela permutação desses dois eventos. Como se trata de um mesmo evento, sua permutação não altera o programa. Sendo assim, é preciso “descontar” 2 possibilidades, ou seja, deve-se dividir o total de permutações simples por esse valor, ou seja, 6! por 2!. A mesma coisa ocorre para a feira de artes: deve-se dividir o total de possibilidades por 2!.
Dessa forma, o total de possibilidades distintas de programas é:
Note que das 6 possibilidades, 2 são cinema e 2 são feira de artes.
O número de permutações de n elementos, dos quais n, é de um tipo, n, é de um segundo tipo, …, n, é de um k-ésimo tipo, é denotado por Pnn1, n2, …,nk, e é dado por
Pnn1, n2, …,nk, = 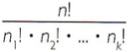
Exemplo:
Quantos anagramas podem ser formados com a palavra MATEMÁTICA?
Observe que são dez letras das quais uma delas se repete três vezes, caso da letra A, e outra que se repete duas vezes, o da letra T. Realizando o cálculo, tem-se:
Com a palavra MATEMÁTICA podem ser formados 302400 anagramas.
Permutação circular
Voltando ao exemplo da reunião que o presidente de uma grande empresa realiza todas as manhãs de segunda-feira com seus cinco diretores, se a mesa na qual é realizada a reunião for redonda, será que as possibilidades de dispor essas pessoas são as mesmas?
A resposta é não. Para visualizar essa situação, pense nas seis pessoas (A, B, C, D, E e F) ao redor da mesa e estabeleça uma ordem entre as 6 = 720 possibilidades, a priori, possíveis. Note que, por exemplo, as ordens ABCDEF, FABCDE, EFABCD, DEFABC, CDEFAB e BCDEFA são seis modos de descrevera mesma posição, pois obtém-se isso girando a mesa. Sendo assim, essas possibilidades devem ser “descontadas”, resultando em:
O número de possibilidades de dispor o presidente e os diretores numa mesa redonda é 120
Esse é um típico exemplo de permutação circular, cuja notação é dada por PC, e cuja definição é:
O número de permutações circulares de n elementos é dado por:
![]()
Por: Miguel de Castro Oliveira Martins