Vamos conhecer uma importante ferramenta matemática que possibilita os cálculos com grandezas físicas vetoriais. Essa ferramenta recebe o nome de vetor e é caracterizada como um segmento de reta orientado.
1 – O VETOR
Considere o segmento orientado AB na figura abaixo.
Observe que o segmento orientado AB é caracterizado por três aspectos bastante definidos:
• comprimento (denominado módulo)
• direção
• sentido (de A para B)
Chama-se vetor ao conjunto infinito de todos os segmentos orientados equipolentes a AB, ou seja, o conjunto infinito de todos os segmentos orientados que possuem o mesmo comprimento, a mesma direção e o mesmo sentido de AB.
Assim, a ideia de vetor nos levaria a uma representação do tipo:
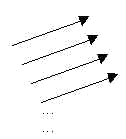
Na prática, para representar um vetor, tomamos apenas um dos infinitos segmentos orientados que o compõe. Guarde esta ideia, pois ela é importante!
Sendo u um vetor genérico, o representamos pelo símbolo:
| Para facilitar o texto, representaremos o vetor acima na forma em negrito u . Todas as representações de letras em negrito neste arquivo, representarão vetores. O módulo do vetor u, será indicado simplesmente por u, ou seja, a mesma letra indicativa do vetor, sem o negrito. |
Podemos classificar os vetores em tres tipos fundamentais:
Vetor livre – aquele que fica completamente caracterizado, conhecendo-se o seu módulo, a sua direção e o seu sentido.
Exemplo: o vetor u das figuras acima.
Vetor deslizante – aquele que para ficar completamente caracterizado, devemos conhecer além da sua direção, do seu módulo e do seu sentido, também a reta suporte que o contém. Os vetores deslizantes são conhecidos também como cursores.
Notação: (u, r) – vetor deslizante (cursor) cujo suporte é a reta r.
Exemplo: ver figura abaixo
Vetor ligado – aquele que para ficar completamente caracterizado, devemos conhecer além da sua direção, módulo e sentido, também o ponto no qual está localizado a sua origem.
Notação: (u, O) – vetor ligado ao ponto O.
Exemplo: ver figura abaixo.
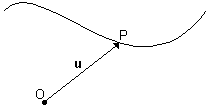
Notas:
a) o vetor ligado também é conhecido como vetor de posição.
b) os vetores deslizantes e os vetores ligados, possuem muitas aplicações no estudo de Mecânica Racional ou Mecânica Geral, disciplinas vistas nos semestres iniciais dos cursos de Engenharia.
c) neste trabalho, ao nos referirmos aos vetores, estaremos sempre considerando os vetores livres
1.1 – O VETOR OPOSTO
Dado o vetor u, existe o vetor – u, que possui o mesmo módulo e mesma direção do vetor u , porém, de sentido oposto.
1.2 – O VETOR UNITÁRIO (VERSOR)
Chamaremos de VERSOR ou VETOR UNITÁRIO, ao vetor cujo módulo seja igual à unidade, ou seja:
| u | = u = 1.
1.3 – O VETOR NULO
Vetor de módulo igual a zero, de direção e sentido indeterminados.
Notação: 0
2 – A PROJEÇÃO DE UM VETOR SOBRE UM EIXO
Veja a figura abaixo, na qual o vetor u forma um ângulo q com o eixo r.
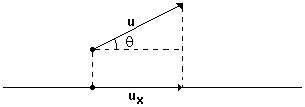
Teremos que o vetor ux será a componente de u segundo o eixo r, de medida algébrica igual a
ux = u . cosq . Observe que se q = 90º, teremos cosq = 0 e, portanto, a projeção do vetor segundo o eixo r, será nula.
3 – A NOTAÇÃO DE GRASSMANN PARA OS VETORES
Considere o vetor u na figura abaixo, sendo A a extremidade inicial e B a extremidade final do vetor.
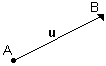Grassmann (matemático alemão – 1809/1877) interpretou a situação, como o ponto B obtido do ponto A, através de uma translação de vetor u.
Assim, pode-se escrever:
B = A + u e, portanto, pode-se escrever também: u = B – A
Esta interpretação, um vetor enxergado como uma diferença de dois pontos, permitirá a simplificação na resolução de questões, conforme veremos na sequência deste trabalho.
4 – UM VETOR NO PLANO COMO UM PAR ORDENADO
Considere o vetor u, representado no plano cartesiano Oxy, conforme figura abaixo:
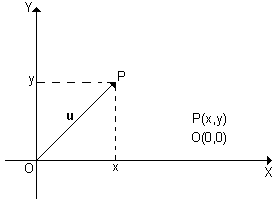
Pela notação de Grassmann, poderemos escrever:
P = O + u
u = P – O
Se considerarmos que o ponto O é a origem do sistema de coordenadas cartesianas e, por conseguinte,
O(0, 0) e que as coordenadas de P sejam x (abcissa) e y (ordenada), teremos o ponto P(x, y).
Substituindo acima, vem:
u = P – O = (x, y) – (0, 0) = (x – 0, y – 0 ) = (x, y).
Portanto,
u = (x, y)
Logo, o vetor u, fica expresso através de um par ordenado, referido à origem do sistema de coordenadas cartesianas.
Neste caso, o módulo do vetor u (aqui representado por u, conforme convenção adotada acima), sendo a distância do ponto P à origem O, será dado por:
5 – UM VETOR NO PLANO, EM FUNÇÃO DOS VERSORES DOS EIXOS COORDENADOS
Vimos acima que um VERSOR, é um VETOR de módulo unitário. Vamos associar um versor a cada eixo, ou seja: o versor i no eixo dos x e o versor j no eixo dos y, conforme figura abaixo:
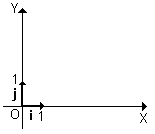
O par ordenado de versores (i, j) constitui o que chamamos de BASE do plano R2, ou seja, base do plano cartesiano Oxy.
Verifica-se que um vetor u = (x, y), pode ser escrito univocamente como:
u = x.i + y.j
Analogamente, se em vez do plano R2, estivéssemos trabalhando no espaço R3, poderíamos considerar os versores i, j e k, respectivamente dos eixos Ox, Oy e Oz, conforme figura abaixo, e a representação do vetor u, no espaço seria:
u = (x, y, z) = x.i + y.j + z.k
Analogamente, o terno (i, j, k), será a BASE do espaço R3 .
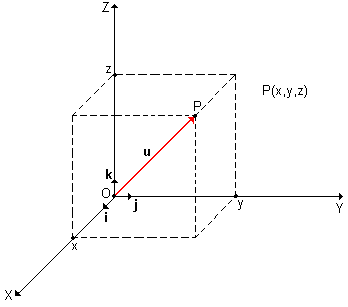
O módulo do vetor u = x.i + y.j + z.k será dado por:
A demonstração desta fórmula é fácil, quando soubermos determinar o produto interno de vetores, conforme você mesmo confirmará na sequência deste trabalho.
6 – OPERAÇÕES COM VETORES
6.1 – ADIÇÃO
Dados dois vetores u e v, define-se o vetor soma u + v, conforme indicado nas figuras abaixo.
Regra do triângulo
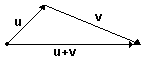
Regra do paralelogramo
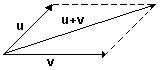
6. 2 – SUBTRAÇÃO
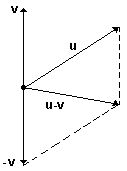
Considerando-se a existência do vetor oposto -v, podemos definir a diferença u – v, como sendo igual
à soma u + ( -v ) .
Veja a figura abaixo:
6.3 – MULTIPLICAÇÃO POR UM ESCALAR
Dado um vetor u e um escalar l Î R, define-se o vetor l .u, que possui a mesma direção de u e sentido coincidente para l > 0 e sentido oposto para l < 0. O módulo do vetor l .u será igual a
|l |.u .
6.4 – PRODUTO INTERNO DE VETORES
Dados dois vetores u e v, define-se o produto interno desses vetores como segue:
u . v = u . v . cos b onde u e v são os módulos dos vetores e b o ângulo formado entre eles.
Da definição acima, infere-se imediatamente que:
a) se dois vetores são paralelos, (b = 0º e cos 0º = 1) então o produto interno deles, coincidirá com o produto dos seus módulos.
b) o produto interno de um vetor por ele mesmo, será igual ao quadrado do seu módulo, pois neste caso,
b = 0º e cos 0º = 1 u.u = u.u.1 = u2
c) se dois vetores são perpendiculares, (b = 90º e cos 90º = 0) então o produto interno deles será nulo.
d) o produto interno de dois vetores será sempre um número real.
e) o produto interno de vetores é também conhecido como produto escalar.
6.4.1 – CÁLCULO DO PRODUTO INTERNO EM FUNÇÃO DAS COORDENADAS DO VETOR
Sejam os vetores u = (a, b) = a i + b j e v = (c, d) = c i + d j
Vamos multiplicar escalarmente os vetores u e v.
u.v = (a i + b j).(c i + d j) = ac i.i + ad i.j + bc j.i + bd j.j
Lembrando que os versores i e j são perpendiculares e considerando-se as conclusões acima, teremos:
i.i = j.j = 1 e i.j = j.i = 0
Daí, fazendo as substituições, vem:
u.v = ac . 1 + ad . 0 + bc . 0 + bd . 1 = ac + bd
Então concluímos que o produto interno de dois vetores, é igual à soma dos produtos das componentes correspondentes ou homônimas.
Unindo a conclusão acima, com a definição inicial de produto interno de vetores, chegamos a uma importante fórmula, a saber:
Sejam os vetores: u = (a,b) e v = (c, d)
Já sabemos que: u.v = u.v.cosb = ac + bd
Logo, o ângulo formado pelos vetores, será tal que:
Onde u e v correspondem aos módulos dos vetores e a, b, c, d são as suas coordenadas.
Portanto, para determinar o ângulo formado por dois vetores, basta dividir o produto interno deles, pelo produto dos seus módulos. Achado o coseno, o ângulo estará determinado.
Veremos um exercício de aplicação, no final deste arquivo.
Vamos demonstrar o teorema de Pitágoras, utilizando o conceito de produto interno de vetores.
Seja o triângulo retângulo da figura abaixo:
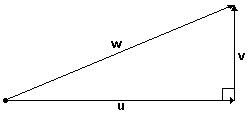
É óbvio que: w = u + v
Quadrando escalarmente a igualdade vetorial acima, vem:
w2 = u2 + 2.u.v + v2
Dos itens (b) e (c) acima, concluímos que w2 = w2, u2 = u2, v2 = v2 e u.v = 0 (lembre-se que os vetores u e v são perpendiculares).
Assim, substituindo, vem:
w2 = u2 + 2.0 + v2, ou, finalmente: w2 = u2 + v2 (o quadrado da hipotenusa é igual à soma dos quadrados dos catetos).
Agora, convidamos ao visitante, a deduzir o o teorema dos cossenos, ou seja : em todo triângulo, o quadrado de um lado é igual à soma dos quadrados dos outros dois lados, menos o dobro do produto desses lados pelo cosseno do ângulo formado entre eles.
Exercícios resolvidos de vetores
Para concluir, vamos resolver algumas questões envolvendo vetores.
1 – Dados os vetores no plano R2, u = 2 i – 5 j e v = i + j, pede-se determinar:
a) o vetor soma u + v
b) o módulo do vetor u + v
c) o vetor diferença u – v
d) o vetor 3 u – 2 v
e) o produto interno u.v
SOLUÇÃO:
a) Temos: u = (2, -5) e v = (1, 1). Logo, u + v = (2, -5) + (1, 1) = (3, -4) = 3 i – 4 j
b) | u + v| = Ö 32 + 42 = Ö 25 = 5 ou 5 u.c (u.c. = unidades de comprimento).
c) u – v = (2, -5) – (1, 1) = (1, -6) = i – 6 j
d) 3u – 2v = 3.(2, -5) -2( 1, 1) = (6, -15) + (-2, -2) = (4, -17) = 4 i – 17 j
e) u.v = 2.1 + (-5).1 = – 3
Autoria: Paulo Marques
