Excentricidade das Cônicas
As cônicas – hipérbole, parábola, elipse e a circunferência, possuem todas elas, um aspecto singular: podem ser obtidas através da interseção de um plano convenientemente escolhido com uma superfície cônica, conforme mostrado na figura a seguir:
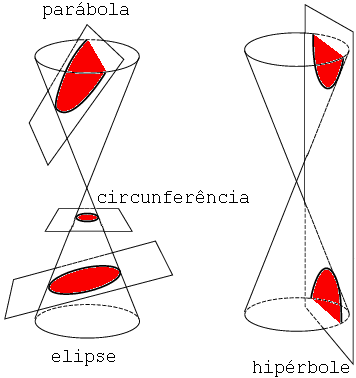
A circunferência é, na realidade, uma elipse perfeita, cuja excentricidade é nula.
No caso da elipse já sabemos que:
excentricidade = e = c/a
Como é válido na elipse que a2 = b2 + c2, vem que:
![]()
Ora, como c < a, vem imediatamente que e < 1. Também, como a e c são distâncias e portanto, positivas, vem que e > 0. Em resumo, no caso da elipse, a excentricidade é um número situado entre 0 e 1 ou seja:
0 < e < 1.
Observa-se que a elipse é tanto mais achatada quanto mais próximo da unidade estiver a sua excentricidade.
Raciocinando opostamente, se o valor de c se aproxima de zero, os valores de a e de b tendem a igualar-se e a elipse, no caso extremo de c = 0, (o que implica e = 0) transforma-se numa circunferência. A circunferência é então, uma elipse de excentricidade nula.
No caso da hipérbole , já sabemos que c2 = a2 + b2 e, portanto,
![]()
Neste caso, c > a, o que significa que a excentricidade de uma hipérbole é um número real maior do que a unidade, ou seja e > 1.
Observe na fórmula acima que se as medidas a e b forem iguais, ou seja a = b, teremos uma hipérbole equilátera, cuja excentricidade será igual a e = Ö 2, resultado obtido fazendo a = b na fórmula acima.
Resumindo, observe que sendo e a excentricidade de uma cônica:
Cônica | e |
Circunferência | 0 |
Elipse | 0 < e < 1 |
Hipérbole | e > 1 |
Quanto à parábola , podemos dizer, que a sua excentricidade será igual a 1? Em a realidade, a excentricidade da parábola é igual a 1; Vamos desenvolver este assunto a seguir:
Considere o seguinte problema geral:
Determinar o lugar geométrico dos pontos P(x, y) do plano cartesiano que satisfazem à condição PF = e . Pd, onde F é um ponto fixo do plano denominado foco e d uma reta denominada diretriz, sendo e uma constante real.
Veja a figura abaixo, para ilustrar o desenvolvimento do tema:
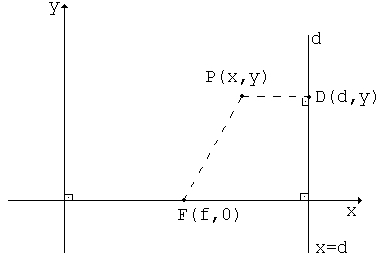
Temos então, pela condição dada, PF = e.Pd, onde e é uma constante real.
Usando a fórmula de distancia entre dois pontos, fica:
![]()
Quadrando e desenvolvendo ambos os membros da expressão acima, vem:
(x – f)2 + y2 = e2 .(x – d)2
x2 – 2.f.x + f2 + y2 = e2 (x2 – 2.d.x + d2)
x2 – e2.x2 – 2.f.x + e2.2.d.x + y2 + f2– e2.d2 = 0
x2(1 – e2) + y2 + (2e2d – 2f)x + f2 – e2.d2 = 0
Ou finalmente:
x2(1 – e2) + y2 + 2(e2d – f)x + f2 – e2d2 = 0
Fazendo e = 1 na igualdade acima, obteremos y2 + 2(d – f).x + f2 – d2 = 0
Fazendo d = – f, vem: y2 – 4fx = 0 ou y2 = 4fx, que é uma parábola da forma y2 = 2px, onde f = p/2, conforme vimos no texto correspondente.
A constante e é denominada excentricidade.
Vê-se pois, que a excentricidade de uma parábola é igual a 1
Algumas Aplicações das Cônicas
O interesse pelo estudo das cônicas remonta a épocas muito recuadas. De fato, estas curvas desempenham um papel importante em vários domínios da física, incluindo a astronomia, na economia, na engenharia e em muitas outras situações, pelo que não é de estranhar que o interesse pelo seu estudo seja tão antigo.
Vejamos então algumas situações onde estas curvas aparecem.
Suponhamos que temos uma lanterna direcionada para uma parede, então o feixe de luz emitido desenhará nessa parede uma curva cónica. Este fato acontece porque o feixe de luz emitido pela lanterna forma um cone, e também porque a parede funciona como um plano que corta o cone formado. Dependendo da inclinação da lanterna relativamente à parede, assim se obtém uma circunferência, uma elipse, uma parábola ou uma hipérbole.
Certos candeiros de cabeceira, cujo quebra luz (abat-jour) é aberto segundo uma circunferência, desenham na parede uma hipérbole e no tecto uma elipse.
Os Engenheiros da área da iluminação usam este fato, entre outros, para construirem candeiros, lanternas, etc…
O som emitido por uma avião a jato supersônico tem a forma de um cone, pelo que, ao chocar com a Terra vai formar uma curva cónica. Assim, dependendo da inclinação do avião relativamente à Terra, vamos obter elipses, parábolas ou hiperboles. A audiometria usa este fato, entre outros, para saber a que distância da Terra o avião pode ultrapassar a velocidade do som.
A superfície formada pela água dentro de um copo é elíptica, sendo circular apenas no caso em que o copo está direito, isto é, está alinhado com o nível, na horizontal.
Se animarmos o copo com um movimento rotativo sobre si próprio, a superfície do líquido nele inserido será a de um paraboloide. Esta técnica é frequentemente usada para se obter este tipo de superficie.
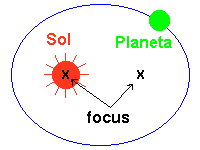
Na astronomia, Kepler mostrou que os planetas do sistema solar descrevem órbitas elípticas, as quais têm o sol num dos focos. Também os satélites artificiais enviados para o espaço percorrem trajetórias elípticas. Mas nem todos os objetos que circulam no espaço têm órbitas elípticas. Existem cometas que percorrem trajetórias hiperbólicas, os quais ao passarem perto de algum planeta com grande densidade, alteram a sua trajetória para outra hipérbole com um foco situado nesse planeta. Como a parábola é um caso de equilibrio entre a elipse e a hipérbole (lembre-se que a excentricidade da parábola é igual a um), a probabilidade de existir algum satélite com órbita parabólica é quase nula. Mas isso não impede a existência de satélites com esta trajetória.
Também as trajetórias dos projéteis, num ambiente sob a ação da força de gravidade, são parabólicas. Já no ambiente terrestre, onde existe a resistência do ar, essas trajectórias são elípticas, mais propriamente, arcos de elipses. No entanto, por vezes, as diferenças entre as trajetórias eliptícas e as parabólicas são quase indiscerniveis, pelo que, pode-se facilmente verificar estes fatos tomando atenção ao jato de água de uma mangueira, cuja a abertura está inclinada para cima. A balística ciência que estuda as trajetória de projéteis, faz uso deste fato para determinar o local da queda de um projétil.
No estudo dos átomos, um campo da Física e da Química, as órbitas dos eletrons em torno do núcleo são elípticas.
antena parabolica
Fazendo uso da propriedade reflectora da parábola, Arquimedes construiu espelhos
parabólicos, os quais por reflectirem a luz solar para um só ponto, foram usados para incendiar os barcos romanos quando das invasões de Siracusa. Lembre-se que a concentração de energia gera calor.
De faco, as propriedades reflectoras das cônicas, e não somente as da parábola, tem contribuido para a construção de telescópios, antenas, radares, farois, ópticas dos carros, lanternas, etc… Na verdade, alguns dos objetos mencionados também obedecem à propriedade refratora das cônicas. Esta propriedade está intimamente ligada à propriedade reflectora, pelo que os seus estudos são muito idênticos. Só para dar uma amostra de objetos mais vulgares que usam a propriedade refratora das cônicas, mencionamos os seguintes: os oculos graduados, as lupas e os microscópios.

A partir da propriedade reflectora das parábolas, os engenheiros civis construiram pontes de suspensão parabólica. Se imaginarmos os cabos que predem o tabuleiro da ponte como raios de luz, facilmente verificamos que o cabo principal, aquele que passa pelos pilares da ponte, tem forma de uma parábola.
As extremidades das asas do famoso avião britanico spitfire, usado com grande sucesso na I grande Guerra, eram arcos de elipses. Embora a razão da sua escolha se prenda ao fato de se obter mais espaço para transportar munições, este tipo de asa diminuia a resistência do ar, favorecendo melhores performances ao avião em voo.
O sistema de localização de barcos denominado por LORAM (LOng RAnge Navigation), faz uso das hipérboles confocais, onde os radares estão nos focos. A ideia é baseada na diferença de tempo de recepção dos sinais emitidos simultaneamente pelos dois pares de radares, sendo um dos radares comum aos dois pares. O mapa assim construido apresenta curvas hiperbólicas. Esta técnica foi usada na II grande Guerra, para detectar barcos japoneses.
Autoria: Paulo Marques