Ao se interpretar um problema, por conta das variáveis e constantes que a circunstância sob uma interpretação apresenta, é possível que ele seja expresso por meio de uma linguagem dotada de símbolos, geralmente, sob a forma de uma equação. Por esse motivo, é possível que se defina uma equação como a consequência da interpretação de uma situação que apresenta um problema, ou, simplesmente, situação-problema.
Para que se possa resolver uma equação é preciso recorrer ao princípio da igualdade, que é, matematicamente falando, uma equivalência entre duas expressões numéricas ou quantidades. Isso implica que quaisquer fatores, para serem iguais, devem ter o mesmo valor.
É natural que se considere como equações elementares as equações de primeiro grau e as equações de segundo grau na medida em que elas fundamentam toda a lógica estrutural dos estudos que envolvem todas as equações matemáticas.
É possível verificar que todas as equações têm um ou mais símbolos que indicam valores não conhecidos, que são chamados de variáveis ou incógnitas. Verifica-se também que em toda equação há um sinal de igualdade (=), uma expressão à esquerda da igualdade, denominada primeiro membro ou membro da esquerda, e uma expressão à direita da igualdade, denominada segundo membro ou membro da direita.
Equação de Primeiro Grau
É possível definir uma equação de primeiro grau como uma equação na qual a potência da incógnita ou das incógnitas é de grau um. A representação geral de uma equação de primeiro grau é:
ax + b = 0
Sendo que: a,b ∈ ℝ e a ≠ 0
Lembrando que o coeficiente a que está na equação é o coeficiente angular e o coeficiente b da equação é o coeficiente linear. De maneira respectiva, seus valores representam a tangente do ângulo de inclinação e o ponto numérico no qual a reta passa pelo eixo das ordenadas, o eixo y.
Para encontrar o valor da incógnita, valor da raiz, de uma equação de primeiro grau é necessário que se isole o x, dessa maneira:
ax + b = 0
ax = – b
x = -b / a
Então, de uma forma geral, o conjunto solução (conjunto verdade) de uma equação de primeiro grau sempre será representado por:
 Equação de Segundo Grau
Equação de Segundo Grau
É possível definir uma equação de segundo grau como uma equação na qual a maior potência da incógnita ou das incógnitas é de grau dois. De forma geral:
ax2 + bx + c = 0
Sendo que: a,b e c ∈ ℝ e a ≠ 0
Raízes de uma Equação de Segundo Grau
Em equações desse tipo é possível encontrar até duas raízes reais, que podem distintas (quando o discriminante é maior que zero) ou iguais (quando o discriminante é igual a zero). É possível também que se encontrem raízes complexas e isso ocorre nos casos em que o discriminante é menor que zero. Lembrando que o discriminante é dado pela relação:
Δ = b² – 4ac
As raízes são encontradas pela chamada “Fórmula de Bhaskara”, que é dada a seguir:
Então, de uma forma geral, o conjunto solução (conjunto verdade) de uma equação de segundo grau sempre será representado por:
S = {x1, x2}
Observações:
- Quando Δ > 0, x1 ≠ x2;
- Quando Δ = 0, x1 = x2;
- Quando Δ < 0, x ∉ℝ.
Uma curiosidade sobre a denominação “Fórmula de Bhaskara” para a relação que dá as raízes de uma equação de segundo grau é que “o nome de Bhaskara relacionado a esta fórmula aparentemente só ocorre no Brasil. Não encontramos esta referência na literatura matemática internacional. A nomenclatura “fórmula de Bhaskara” não é adequada, pois problemas que recaem numa equação do segundo grau já apareciam quase quatro mil anos antes, em textos escritos pelos babilônios, nas tábuas cuneiformes”.
É possível também encontrar as raízes de uma equação de segundo grau por meio das Relações de Girard, que popularmente são chamadas de “soma e produto”. As Relações de Girard mostram que há razões estabelecidas entre os coeficientes que nos permitem encontrar a soma ou o produto das raízes de uma equação de segundo grau. A soma das raízes é igual a razão – b / a e o produto das raízes é igual a razão c / a, como exposto abaixo:
S = x1 + x2 = – b / a
P = x1 . x2 = c / a
Por meio das relações dadas acima é possível construir as equações a partir de suas raízes:
x² – Sx + P = 0
Demonstração:
- Dividindo todos os coeficientes de ax² + bx + c = 0 se obtém:
(a/a)x² + (b/a)x + c/a = 0/a ⇒ (a/a)x² – (-b/a)x + c/a = 0/a ⇒1x² – (-b/a) + (c/a) = 0
- Como a soma das raízes é S = – b/a e o produto das raízes é P = c/a, então:
x² – Sx + P = 0
Referência Bibliográfica
IEZZI, Gelson, MURAKAMI, Carlos. Fundamentos de Matemática Elementar – 1: Conjuntos e Funções.São Paulo, Editora Atual, 1977
http://ecalculo.if.usp.br/historia/bhaskara.htm
https://repositorio.ufsc.br/bitstream/handle/123456789/96543/Taciana_Zardo.pdf?sequence=1
http://www.irem.univ-rennes1.fr/recherches/groupes/groupe_algo/ALGO2009_11_Activites/algo1_babylone.pdf
Por: Anderson Andrade Fernandes
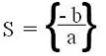 Equação de Segundo Grau
Equação de Segundo Grau