Há três ramos principais da estatística: estatística descritiva, que envolve a organização e a dados; a teoria da probabilidade, que proporciona uma base racional para lidar com situações influenciadas por fatores relacionados com o acaso, assim como estimar erros; e a teoria da inferência, que envolve análise e interpretação de amostras.
A Estatística, de modo geral, constitui um valioso instrumento para tomada de decisões.
Outra característica da Estatística é o uso de modelos. Estes são formas simplificadas de algum problema ou situação real. A característica fundamental dos modelos é o fato de reduzirem situações complexas a formas mais simples e mais compreensíveis.
Estatística é uma parte da Matemática Aplicada que fornece métodos para a coleta, organização, descrição, análise e a interpretação de dados e para a utilização dos mesmos na tomada de decisões (Antônio Amot, 2002).
Estatística Dedutiva – é responsável pela coleta, organização e a descrição dos dados.
Estatística Indutiva ou Inferencial – responsável pela análise e a interpretação desses dados. Possibilitam o diagnóstico de um lugar, o conhecimento de seus problemas,a formulação de soluções apropriadas e um planejamento objetivo de ação.
Amostra: grupo representativo de uma classe,ou melhor, é um subconjunto finito de uma população (Antônio Arnot,2002), deve possuir as mesmas características básicas da população, em relação ao que deseja pesquisar.
Principais técnicas de amostragem:
1º Amostragem casual ou aleatória simples
2º Amostragem proporcional estratificada
3º Amostragem sistemática
Amostra homogenia – mais fácil de obter resultados
Amostra heterogenia – mais difícil de obter resultados.
Dados: informações necessárias para representar a estatística.
Dados brutos: são os primeiros dados obtidos.
Dados seriados: são dados organizados e apurados por uma série para que ele passe por uma análise e por fim a resolução de um problema.
Dados Primários: são os dados obtidos pelo próprio pesquisador.
Dados Secundários: são dados obtidos por outros pesquisadores.
Variável é considerada como um conjunto de resultados possíveis de um fenômeno, Do ponto de vista da natureza ela pode ser:
1- Qualitativa: quando seus valores são expressos por atributos;
2- Quantitativa: quando seus valores são expressos em números;
- Variável contínua: qualquer valor entre dois limites, permite divisões, se costuma fazer divisões, são originadas das medições;
- Variável discreta: só pode assumir valores pertencentes a um conjunto de enumerável, toda variável advém de um número, devido sua contagem, é exato, tem origem nas contagens ou enumerações;
Sendo atributo, pode ser:
1- Dicotômicos: permitem apenas 2 alternativas;
2- Policotomicas: com muitas possibilidades de alternativas;
Aproximação dos resultados:
– Fração acima da metade (0,5): aproxima-se o valor para o número seguinte.
Ex: 2,8 → 3,0
– Fração menor da metade (0,5): aproxima-se o valor para o número abaixo.
Ex: 2,3 → 2,0
– Quando a fração for a metade (0,5): aproxima-se o valor para o número par.
Ex: 2,5 → 2,0
1,5 → 2,0
Para atingir uma estatística é necessário:
- Definir Problema;
- Planejamento da obtenção de dados;
- Coleta de dados;
- Sistematização ou organização;
- Seriação
- Análise e interpretação de dados;
- Resolução de problemas;
Exemplo aplicado
No 1º semestre de 2003, os estudantes de Psicologia da FTC, iniciaram um Projeto Interdisciplinar na Comunidade da Bananeira, onde a turma foi dividida em 8 equipes e cada uma delas ficou responsável pela coleta de dados de determinadas células ou famílias, buscando conhecer o meio, identificar o número de moradores de cada casa, seu histórico, sexo e idade.
O exemplo aqui apresentado, foi coletado no 1º semestre de 2003, onde procura-se identificar o número de moradores das células e a idade.
Dados Brutos: são os primeiros dados obtidos.
Rol: organização dos dados por ordem de valor, sendo ele crescente ou decrescente.
Amplitude total (AT): dispersão entre o maior e o menor número, no caso a idade.
Quanto maior a amplitude, mais heterogêneo é o grupo.
Número de classes (NC): o pesquisador é quem define, não sendo menor que 4 nem maior que 10.
Amplitude de classe(AC): divide-se a amplitude total pela amplitude de classes.
Aplicação:
Dados Brutos: Rol: Amplitude Total:
94 94 94 – 14= 80
68 72
72 68 Número de classes:
45 45 NC=4
22 34
19 22 Amplitude de Classes:
16 19 AC = AT/NC = 80/20
14 16 AC = 4
34 14
As tabelas e os gráficos fornecem rápidas e seguras informações a respeito das variáveis em estudo, permitindo determinações administrativas e pedagógicas mais coerentes e científicas.
A Tabela é um quadro que resume um conjunto de observações.
Classes: serve para reunir grandes massas de dados
Limites de classe – os números externos de uma classe;
- 14 |– 34: 14 pertence;
- 34 |– 54: 34 pertence;
- 14 |–| 94: ambos pertencem à classe.
Frequência: número de valores das variáveis pertencentes a cada uma das classes.
FAC: Frequência acumulada crescente, (5+1+2+1) = (5,6,8,9).
FAD: Frequência acumulada decrescente, (5-1-2-1)=(9,,4,3,1)
FR: Frequência relativa, fazer uma relação entre o número total de moradores e a frequência.
Ponto Médio: número pedido de intervalo entre as classes.
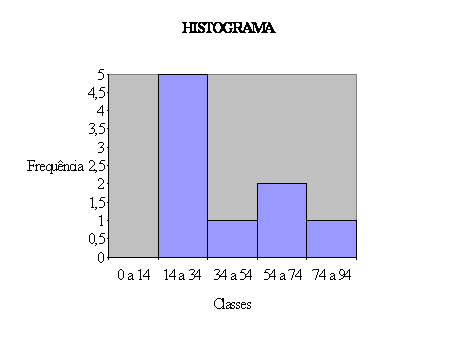
O Histograma é o tipo de gráfico mais amplamente utilizado, é constituído desenhando-se barras, cujas bases são determinadas pelos intervalos de classe e cujas alturas são determinadas pelas correspondentes frequências de classe.
BIBLIOGRAFIA
CRESPO. Antônio A. Estatística Fácil. 18º ed. São Paulo: Saraiva 2002.