Todo número composto pode ser expresso de forma única como produto de números primos distintos elevados a potências. Esse procedimento chama-se fatoração.
Fatoração de um número
Fatorar um número é decompô-lo em produto de fatores primos. Para isso, divide-se o número entre seus divisores primos tantas vezes quantas forem necessárias, até obter como quociente a unidade. Começa-se dividindo por 2, depois por 3, por 5, por 7, por 11, e assim por diante. O processo termina expressando o número como produto de seus fatores primos.
Exemplos:
- ex. 1 – Decompor o número 60 como produto de seus fatores primos. Números primos: 2, 3, 5, 7, 11…
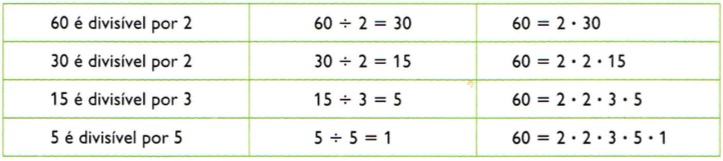
Pode-se expressar o número 60 como:
60 = 2 • 2 • 3 • 5 = 22 • 3 • 5
Utiliza-se o método da decomposição fatorial vertical.
Números primos: 2, 3, 5, 7, 11…
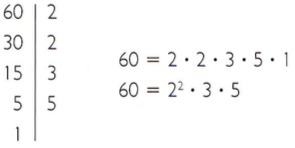
- ex. 2 – Decomporem fatores primos 81 e 32.
Como obter todos os divisores de um número?
1. É preciso obter a decomposição do número em produto de fatores primos. Todo número pode ser expresso de forma única como produto de números primos distintos elevados a potências.
Decompor 36 da seguinte forma:
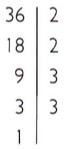36 é composto, já que termina em algarismo par Portanto, é divisível por 2.
Tem-se que 36 = 2 . 18.
18 é composto e é divisível por 2; ou seja, 18 = 2 · 9.
9 é composto e é divisível por 3, ou seja, 9 = 3 · 3.
O número 3 é primo, logo a decomposição termina.
A decomposição do número 36 é 36 = 2 • 2 • 3 • 3 = 22 • 32.
2. Constrói-se a linha A com o número l e as potências sucessivas do primeiro fator primo da decomposição (2) até atingir o expoente obtido na decomposição.
3. Multiplica-se cada número da linha A pela menor potência do fator primo seguinte, que é 31 = 3. Assim, obtém-se a linha B.
4. Multiplica-se a linha A pela seguinte potência do fator primo 3, ou seja, por 32, e obtém-se a linha C. (…)
No caso de existir outro fator primo diferente dos anteriores, repetem-se os passos 2, 3 e 4, multiplicando todas as linhas pelas sucessivas potências.
O conjunto dos divisores de 36 é o formado pelos números de todas as linhas. D (36): 1, 2, 3, 4, 6, 9, 12, 18, 36.
Exemplo:
Calcular os divisores dos números 90 e 54.
Primeiro, decompõem-se os números em fatores primos.
Em seguida, escrevem-se as linhas de números como indica o procedimento do texto.
- D (90): 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45,90.
- D (54); 1, 2, 3, 6, 9, 18, 27, 54.
Por: Osvaldo Shimenes Santos
Veja também:
- Exercícios de Fatoração
- Números Primos e Compostos
- Critérios de Divisibilidade
- Como calcular o MDC – Máximo Divisor Comum
- Como calcular o MMC – Mínimo Múltiplo Comum
