Também denominada função afim ou função polinomial do primeiro grau, a função de primeiro grau é aquela que apresenta a forma f(x) = ax + b (ou y = ax + b), em que a e b representam números reais e a ≠ 0. As funções desse tipo são assim denominadas porque o maior expoente da variável x é 1.
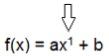
Numa função do primeiro grau, o número real que corresponde ao a sempre multiplica x, recebendo o nome de coeficiente angular, enquanto b é o termo independente, chamado de coeficiente linear. O coeficiente a não pode ser igual a 0 porque, multiplicando x por 0 teremos, evidentemente, o resultado 0, logo, a função tomará a forma f(x) = b, não podendo ser definida como uma função do primeiro grau.
Quando a > 0 (positivo), a função ax + b será do tipo crescente, ou seja, o valor de f(x) cresce à medida que o valor de x aumenta. Por outro lado, quando a < 0 (negativo), a função será do tipo decrescente, isto é, quando o valor de x aumenta, o valor de f(x) diminui.
O gráfico que representa uma função do primeiro grau é sempre uma reta, que será crescente se o coeficiente a for positivo e será decrescente se a for negativo. Nessa representação gráfica, o coeficiente b determinará o ponto onde a reta tocará o eixo vertical. Veja um exemplo:
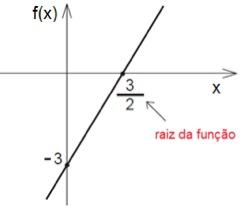
Observando a expressão já será possível perceber que a reta do gráfico será crescente, pois a é positivo. Na função, o valor de b é -3, portanto, o eixo vertical será cortado no ponto -3. Para determinar o ponto em que o eixo horizontal será cortado, precisamos calcular a raiz ou zero da função, que corresponde ao valor de x capaz de tornar f(x) igual a 0.
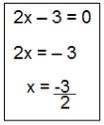Assim, teremos o gráfico da função f(x) = 2x – 3:
Para desenhar o gráfico da função, também podemos atribuir a x dois valores quaisquer e, então, calcular os valores que equivalem a f(x). Na função f(x) = ½ x + 1, determinando que x=0 e x=4, teremos o seguinte gráfico:
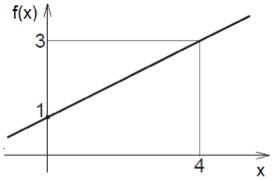
Perceba no gráfico que, quando x vale 0, f(x) vale 1 (½ . 0 + 1 = 1), ao passo que, quando x tem valor 4, f(x) tem valor 3 ( ½ . 4 + 1 = 3). Independente do valor assumido por x, a função sempre expressará o valor de f(x) em função de x.
Na prática, podemos usar as funções de primeiro grau quando um valor se dá em função de outro. Por exemplo:
Nos Estados Unidos, as temperaturas são dadas em graus Fahrenheit (°F), ao contrário do Brasil, onde se utiliza a escala Celsius (°C). Para converter um valor de temperatura de Fahrenheit para Celsius, basta aplicar a seguinte fórmula:
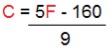
Sabendo que o ponto de fusão da água é 0 °C e de ebulição é 100 °C, determine graficamente os valores correspondentes em °F.
Resolução:
Observe que se trata de uma função do primeiro grau:
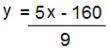
Para encontrarmos os valores em Fahrenheit basta substituir y por 0 e por 100.
No gráfico desta função, a reta deve cortar os pontos (32, 0) e (212, 100). Logo, teremos:
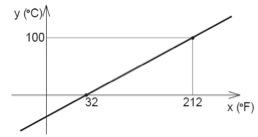
Nesta função, o coeficiente angular é 
, ao passo que o coeficiente linear é 
.
Referências
BONJORNO, José Roberto, GIOVANNI, José Rui. Matemática Completa. São Paulo: FTD, 2005.
http://ftcciv1an.files.wordpress.com/2009/08/telecurso-2000-matematica-ensino-medio.pdf
Por: Mayara Lopes Cardoso
