Inequação produto
Inequação produto é uma inequação que apresenta o produto de duas sentenças matemáticas na variável x, f(x) e g(x), e que pode ser expressa em uma das seguintes formas:
f(x) ⋅ g(x) ≤ 0
f(x) ⋅ g(x) ≥ 0
f(x) ⋅ g(x) < 0
f(x) ⋅ g(x) > 0
f(x) ⋅ g(x) ≠ 0
Exemplos:
a. (x – 2) ⋅ (x + 3) > 0
b. (x + 5) ⋅ (– 2x + 1) < 0
c. (– x – 1) ⋅ (2x + 5) ≥ 0
d. (– 3x – 5) ⋅ (– x + 4) ≤ 0
Cada inequação citada anteriormente pode ser vista como uma desigualdade que envolve o produto de duas sentenças matemáticas de funções reais na variável x. Cada inequação é conhecida como inequação produto.
A quantidade de sentenças matemáticas envolvidas no produto pode ser qualquer uma, embora nas exemplificações anteriores tenhamos apresentado somente duas.
Como resolver uma inequação produto
Para entender a resolução de uma inequação produto, vamos analisar o seguinte problema.
Quais são os valores reais de x que satisfazem a inequação: (5 – x) ⋅ (x – 2) < 0?
Resolver a inequação produto anterior consiste em determinar todos os valores de x que satisfaçam a condição f(x) ⋅ g(x) < 0, sendo f(x) = 5 – x e g(x) = x – 2.
Para isso, vamos estudar os sinais de f(x) e g(x), organizá-los em uma tabela, que chamaremos de quadro de sinais, e, por meio do quadro, avaliar os intervalos em que o produto é negativo, nulo ou positivo, escolhendo por fim o intervalo que resolve a inequação.
Analisando o sinal de f(x):
f(x) = 5 – x
Raiz: f(x) = 0
5 – x = 0
x = 5, raiz da função.
O coeficiente angular é –1, que é um número negativo. Assim, a função é decrescente.
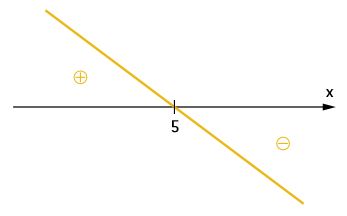
Analisando o sinal de g(x):
g(x) = x – 2
Raiz: f(x) = 0
x – 2 = 0
x = 2, raiz da função.
O coeficiente angular é 1, que é um número positivo. Assim, a função é crescente.
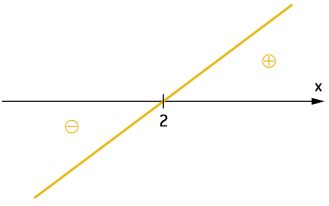
Para determinarmos a solução da inequação, faremos uso do quadro de sinais, colocando os sinais das funções, um em cada linha. Observe:
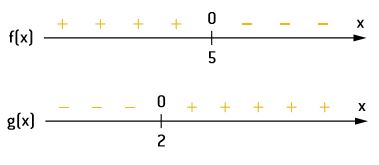
Acima das retas estão os sinais das funções para cada valor de x, e, abaixo das retas, estão as raízes das funções, valores que as zeram. Para representar isso, colocamos, acima dessas raízes, o número 0.
Agora, vamos iniciar a análise do produto dos sinais. Para valores de x maiores do que 5, f(x) tem sinal negativo e g(x) tem sinal positivo. Logo, o produto delas, f(x) ⋅ g(x), será negativo. E, para x = 5, o produto é zero, pois 5 é raiz de f(x).
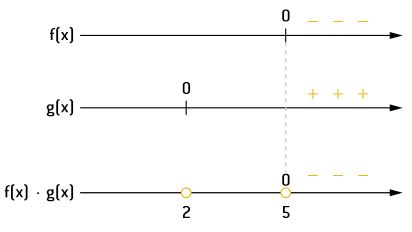
Para qualquer valor de x entre 2 e 5, temos f(x) positivo e g(x) positivo. Logo, o produto será positivo. E, para x = 2, o produto é zero, pois 2 é raiz de g(x).
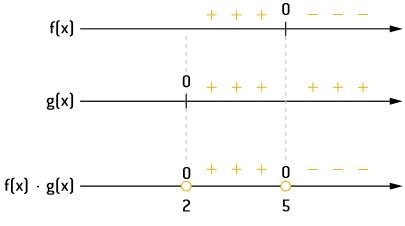
Para valores de x menores do que 2, f(x) tem sinal positivo e g(x) tem sinal negativo. Logo, o produto delas, f(x) ⋅ g(x), será negativo.
Assim, os intervalos em que o produto será negativo estão representados graficamente a seguir.
E, para finalizar, o conjunto solução é dado por:
S = {x ∈ ℜ | x < 2 ou x > 5}.
Inequação quociente
Inequação quociente é uma inequação que apresenta o quociente de duas sentenças matemáticas na variável x, f(x) e g(x), e que pode ser expressa em uma das seguintes formas:
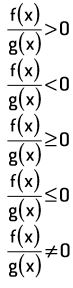
Exemplos:
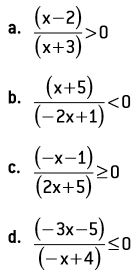
Essas inequações podem ser vistas como desigualdades que envolvem o quociente de duas sentenças matemáticas de funções reais na variável x. Cada inequação é conhecida como inequação quociente.
Como resolver inequações quociente
A resolução da inequação quociente é semelhante ao da inequação produto, uma vez que a regra de sinais na divisão de dois termos é igual à regra de sinais na multiplicação de dois fatores.
É importante, porém, ressaltar que, na inequação quociente: nunca poderá(ão) ser usada(s) a(s) raiz(raízes) proveniente(s) do denominador. Isso ocorre porque, no conjunto dos reais, não está definida a divisão por zero.
Vamos resolver o seguinte problema que envolve inequação quociente.
Quais são os valores reais de x que satisfazem a inequação: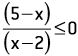
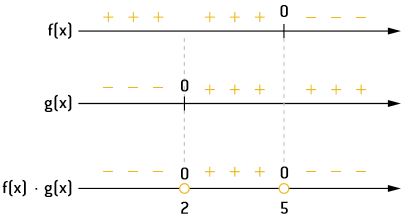
As funções envolvidas são as mesmas do problema anterior e, consequentemente, os sinais nos intervalos: x < 2; 2 < x < 5 e x > 5 são iguais.
Contudo, para x = 2, temos f(x) positivo e g(x) igual a zero, e a divisão f(x)/g(x) não existe.
Devemos, assim, ter cuidado em não incluir x = 2 na solução. Para isso, utilizaremos uma “bolinha vazia” em x = 2.
Em contrapartida, em x = 5, temos f(x) igual a zero e g(x) positivo, e a divisão f(x)/g(x existe e é igual a zero. Como a inequação permite que o quociente tenha valor zero:
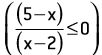
x =5 deve fazer parte do conjunto solução. Assim, devemos colocar “bolinha cheia” em x = 5.
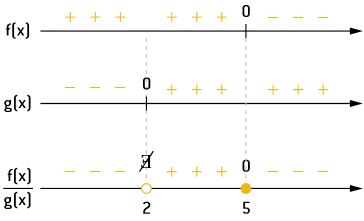
Dessa forma, os intervalos em que o produto será negativo estão representados graficamente a seguir.

S = {x ∈ ℜ | x < 2 ou x ≥ 5}
Note que, se ocorrerem mais de duas funções nas inequações, o procedimento é semelhante, e o quadro dos sinais aumentará a quantidade de funções componentes, conforme a quantidade de funções envolvidas.
Por: Wilson Teixeira Moutinho