As Médias são essenciais para fazer estimativas de tendências de crescimento populacional, de taxas de rendimento em investimentos ao longo de um dado tempo, velocidade média ou, até mesmo, para aplicar na geometria plana e espacial.
Média Aritmética
Média Aritmética Simples:
É a soma dos valores dos elementos dividida pelo número de elementos. Considere os elementos a1, a2, a3, a4… an > 0
MA = ( a1+ a2 + a3 + a4 +… + an )/ número de elementos
Média Aritmética Ponderada:
É a soma dos produtos dos valores dos elementos pela quantidade de vezes que estes se repetem dividida pela soma da quantidade de vezes que os elementos se repetem.
Observe:
Repetições | Elementos |
| qa1 | a1 |
| qa2 | a2 |
| qa3 | a3 |
| qa4 | a4 |
| qan | na |
Considere os elementos a1, a2, a3, a4, …, an > 0 e suas respectivas repetiçõesqa1, qa2, qa3, qa4, …, qan > 0, então:
MA = (a1 x qa1)+(a2 x qa2)+(a3 x qa3)+(a4 x qa4)+… +(na x qan )/qa1 + qa2 + qa3 + qa4 + … + qan
Verifica-se que a Média Aritmética Simples não traduz precisamente diferenças de desempenho, crescimento populacional etc., por esta considerar que todos os elementos componentes de uma Média possuem o mesmo peso, ou seja, a Média Aritmética Simples não considera repetições dos elementos que compõem a Média, tampouco as variações destes mesmos elementos ao longo do tempo. Por isso, ela é mais precisa para mostrar retornos numéricos de problemas que não envolvam repetições dos elementos constituintes da Média ou grandes variações entre os valores destes elementos ao longo do tempo. Nestes casos, Média Aritmética Ponderada mostra resultados mais precisos.
Exemplos:
Exemplos de Média Aritmética Simples e Média Aritmética Ponderada, respectivamente:
Em um departamento de uma empresa qualquer, um funcionário recebe um salário de R$ 1.000,00 por mês, enquanto outro recebe R$ 12.500,00 por mês. Qual é a média salarial mensal destes funcionários?
- MA = ( a1+ a2 + a3 + a4 +… + an )/ número de elementos
- a1= 1000, a2 = 12500 e número de elementos/funcionários = 2
Então: Média Salarial Mensal = 1000 + 12500/ 2 = 6750
Verifica-se que o valor obtido por meio da Média Aritmética Simples não possui uma correspondência verossímil com salários apresentados. Vamos verificar, no próximo exemplo, se haverá essa discrepância entre os valores apresentados e a média:
Verifique a tabela a seguir e, com base nos dados nela contidos, calcule a média salarial mensal:
| Quantidade de Funcionários | Salários / mês (em R$) |
| 15 | 800,00 |
| 3 | 3.000,00 |
| 2 | 5.250,00 |
| 1 | 12.100,00 |
Como há repetições do mesmo valor salarial, ou seja, mais de um funcionário recebe o mesmo salário, o uso da Média Aritmética Ponderada é mais indicado. Por isso, sendo:
MA = (a1 x qa1)+(a2 x qa2)+(a3 x qa3)+(a4 x qa4)+… +(na x qan )/qa1 + qa2 + qa3 + qa4 + … + qan
- a1 = 800, a2 = 3000, a3 = 5250 e a4 = 12.100;
- qa1 = 15, qa2 = 3, qa3 = 2 e qa4 = 1.
Então: Média = (800 x 15) + (3000 x 3) + (5250 x 2) + (12100 x 1) / 15 + 3 + 2 + 1
Média = 12000 + 9000 + 10500 + 12100 / 21 ? 2076, 19
Se os funcionários hipotéticos confrontassem seus salários e as médias mensais dos seus salários com os outros funcionários, certamente, ninguém concordaria com tais valores, tanto os que ganham mais quanto os que ganham menos. Por essa razão, consideramos as Médias Aritméticas (simples ou ponderadas) apenas como uma tentativa de minimizar as relações entre duas ou mais medidas, não tendo muita utilidade prática, a não ser em situações nas quais exista uma grande quantidade de elementos a medir e se faz necessário determinar apenas uma amostra para lidar com o tema abordado. Por consequência, as Médias Geométricas e as Médias Harmônicas possuem mais utilidade prática.
Médias Geométricas
Possuem aplicações práticas em geometria e em matemática financeira. São dadas pela relação: n?( a1 x a2 x a3 x a4 x… an), sendo o índice n correspondente ao número de elementos que, multiplicados entre si, compõem o radicando.
Aplicações na Geometria
É muito comum se fazer uso das Médias Geométricas em geometria plana e espacial:
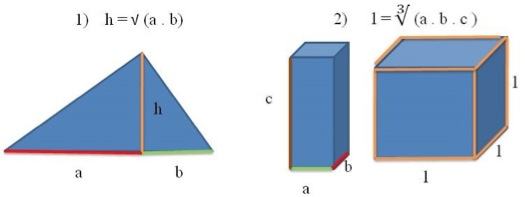
1) Podemos interpretar a Média Geométrica de três números a, b e c como a medida l da aresta de um cubo, cujo volume é o mesmo de um prisma retangular reto, desde que este tenha arestas medindo exatamente a, b e c.
2) Outra aplicação se dá no triângulo retângulo, cuja Média Geométrica das projeções dos catetos (representadas na figura a seguir por a e b) sobre a hipotenusa é igual à altura relativa à hipotenusa. Veja a representação dessas aplicações nas figuras abaixo:
Aplicação na Matemática Financeira
A Média Geométrica é frequentemente usada quando discutimos taxas de rendimento em investimentos. Segue um exemplo a seguir:
Um investimento rendeu anualmente conforme a seguinte tabela:
| 2012 | 2013 | 2014 |
| 15% | 5% | 7% |
Para obtermos a média anual de rendimento desse investimento, basta aplicarmos a Média Geométrica com radical de índice três e radicando composto pelo produto dos três percentuais, ou seja:
Rendimento Anual =?(15% x 5% x 7%) ? 8%
Médias Harmônicas
Médias Harmônicas são usadas quando temos que lidar com uma série de valores inversamente proporcionais como um cálculo de uma velocidade média, um custo médio de compras com uma taxa fixa de juros e resistências elétricas em paralelo, por exemplo. Podemos as Médias Harmônicas da seguinte forma:
Sendo n o número dos elementos e ( a1+ a2 + a3 + a4 +… + an ) o conjunto de elemento envolvidos na média, temos:
Média Harmônica = n / (1/a1+ 1/a2 + 1/a3 + 1/a4 +… + 1/an)
Podemos exemplificar essa a representação mostrando relação a entre a resistência total, RT, de um sistema em paralelo e a soma das suas resistências, R1 eR2, por exemplo. Temos: 1/ RT = (1/R1 + 1/R2), uma relação com o inverso das resistências. Nas relações entre velocidade e tempo, que são inversamente proporcionais, é muito comum usarmos a Média Harmônica. Perceba que se, por exemplo, um veículo faz metade da distância de um trajeto qualquer a 90 km/h e a outra metade a 50 km/h, a velocidade média do trajeto será:
Vm = 2 partes do trajeto / (1/90 km/h + 1/50 km/h)? 64,3 km/h
Perceba que se usarmos a Média Aritmética Simples haverá uma diferença de aproximadamente 6 km/h, faça os cálculos e verifique você mesmo.
Conclusão
Apesar do conceito de Média ser extremamente simples, é importante saber identificar as situações adequadamente para uma aplicação correta de cada tipo de relação envolvendo os conceitos de Média, pois uma aplicação incorreta pode gerar erros relevantes e estimativas discrepantes com a realidade.
REFERÊNCIAS BIBLIOGRÁFICA
VIEIRA SOBRINHO, José Dutra. Matemática Financeira. São Paulo: Atlas, 1982.
http://www.uel.br/projetos/matessencial/superior/calculo/maxmin/mm04.htm (visto em 06/07/2014, às 15:00)
http://www.mathalino.com/reviewer/derivation-of-formulas/relationship-between-arithmetic-mean-harmonic-mean-and-geometric-mea (visto em 05/07/2014, às 11:31)
http://economistatlarge.com/finance/applied-finance/differences-arithmetic-geometric-harmonic-means (visto em 07/07/2014, às 08:10)
http://faculty.london.edu/icooper/assets/documents/ArithmeticVersusGeometric.pdf (visto em 07/07/2014, às 15:38)
Por: Anderson Andrade Fernandes