Chama-se de progressão aritmética (P.A.), toda sucessão de números que, a partir do segundo, a diferença entre cada termo e o seu antecessor é constante.
Vamos considerar as sequências numéricas:
a) (2, 4, 6, 8, 10, 12).
Veja que a partir do 2º termo a diferença entre cada termo e o seu antecessor, é constante:
a2 – a1 = 4 – 2 = 2; a3 – a2 = 6 – 4 = 2
a5 – a4 = 10 – 8 = 2 a6 – a5 = 12 – 10 = 2
b) 
a2 – a1 = 
;
a3 – a2 = 
a4 – a3 = 
a5 – a4 = 
Quando observamos que essas diferenças entre cada termo e o seu antecessor, é constante, damos o nome de progressão aritmética (P.A.) À constante damos o nome de razão (r).
Obs.: r = 0 
P.A. é constante.
r > 0P.A. é crescente.
r < 0P.A. é decrescente.
De um modo geral temos:
Sucessão: (a1, a2, a3, a4, a5, a6, a7, …, an, …)
a2 – a1 = a3 – a2 = a4 – a3 = …= an – an -1 = r
FÓRMULA DO TERMO GERAL DE UMA P.A
Vamos considerar a sequência (a1, a2, a3, a4, a5, a6, a7, …, an) de razão r, podemos escrever:
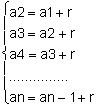
Somando membro a membro essas n – 1 igualdades, obtemos:
a2 + a3+ a4+ an -1 + an = a1+ a2+ a3+ … an -1+ (n-1).r
Após a simplificação temos a fórmula do termo geral de uma P.A.: an = a1 + (n – 1).r
Nota Importante: Quando procuramos uma progressão aritmética com 3, 4 ou 5 termos, podemos utilizar um recurso bastante útil.
• Para 3 termos: (x, x+r, x+2r) ou (x-r, x, x+r)
• Para 4 termos: (x, x+r, x+2r, x+3r) ou (x-3y, x-y, x+y, x+3y). Onde y = 
• Para 5 termos: (x, x+r, x+2r, x+3r, x+4r) ou (x-2r, x-r, x, x+r, x+2r)
INTERPOLAÇÃO ARITMÉTICA
Interpolar ou inserir k meios aritméticos entre dois números a1 e an, significa obter uma progressão aritmética de k+2 termos, cujos os extremos são a1 e an.
Pode-se dizer que todo problema que envolve interpolação se resume em calcularmos a razão da P.A.
Ex.: Veja esta P.A. (1, …, 10), vamos inserir 8 meios aritméticos, logo a P.A. terá 8+2 termos, onde:
a1 = 1; an = 10 ; k = 8 e n = k + 2 = 10 termos.
an = a1 + (n-1).r r = 
a P.A. ficou assim: (1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
SOMA DOS n TERMOS DE UMA P.A. (Sn)
Vamos considerar a P.A.: (a1, a2, a3, …, an-2, an-1, an) (1).
Agora vamos escrevê-la de uma outra forma: (an, an-1, an-2, …, a3, a2, a1) (2).
Vamos representar por Sn a soma de todos os membros de (1) e também por Sn a soma de todos os membros de (2), já que são iguais.
Somando (1) + (2), vem:
Sn = a1 + a2 + a3 + … + an-2 + an-1 + an
Sn = an + an-1 + an-2 +…+ a3 + a2 + a1
2Sn = (a1 + an) + (a2 + an-1) + (a3 + an-2) … + (an-1 + a2) + (an + a1)
Observe que cada parênteses representa a soma dos extremos da progressão aritmética, portanto representa a soma de quaisquer termos equidistantes dos extremos. Então:
2Sn = (a1 + an) + (a1 + an) + … +(a1 + an) + (a1 + an)
n – vezes
2Sn = 
que é a soma dos n termos de uma P.A.
