Há muitas situações cotidianas, seja na vida cotidiana, na ciência ou negócios que requerem o uso de razões e proporções. Por exemplo, na cozinha, se há a intenção de acrescentar ou diminuir algum ingrediente, as razões e proporções são usadas para determinar isso – “3 ovos para cada suas duas colheres de farinha”.
Pode-se verificar outro uso quando farmacêuticos ministram medicamentos, eles devem ter muita atenção às proporções dos fármacos.
Razão
A etimologia latina de razão, ratio, não possui ralação com a ideia de faculdade que permite a distinguir a relação entre as coisas da realidade ou juízo, mas sim a ideia de quociente, divisão, a noção que a matemática assimilou. Por isso, razão é o quociente entre dois números A e B, com B ≠ 0. Assim, a razão entre os números A e B pode ser dita “razão de A para B” e representada como:
Uma razão também pode identificada pela representação A : B. É importante saber que, em uma razão, A sempre será chamado de antecedente, enquanto B será sempre chamado de consequente.
Exemplo:
Se uma bicicleta possui 54 dentes em uma coroa dianteira e 27 dentes na coroa traseira, a razão da marcha da bicicleta será 54 : 27 ou 2 : 1. Isso significa que a roda traseira gira duas vezes cada vez que o pedal gira uma vez. Então, se a razão for de 54 : 11, por exemplo, a roda traseira vai girar aproximadamente cinco vezes para cada vez que o pedal girar.
Proporção
Dados quatro números racionais A, B, C e D diferentes de zero, proporção é a expressão que indica uma igualdade entre duas ou mais razões e pode ser expressa da seguinte forma:
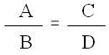
Uma proporção também pode ser expressa como a igualdade entre os produtos (A . D) e (B . C), da seguinte forma: A.D = B.C.
É importante saber que os números A, B, C e D são denominados termos, sendo que os números A e B são os dois primeiros termos e os números C e D são os dois últimos termos da relação de proporção. Os números A e C são os antecedentes de cada razão, enquanto os números B e D são os consequentes de cada razão que compõem a relação de proporção. Em uma relação de proporção A e Dsão os extremos B e Csão os meios. Além disso, a divisão entre A e B e a divisão entre C e D, é uma constante K, denominada constante de proporcionalidade K da razão.
Quarta Proporcional
Dados três números A, B e C, nesta ordem, é um número X para completar com os outros três uma relação de proporção, obtém-se:
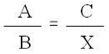
Observando a relação acima é possível concluir que a Quarta Proporcional é, simplesmente a chamada Regra de Três.
Proporção Contínua
É aquela que tem os termos meios iguais: A.D = B.C, com B = C. O valor comum dos meios é chamado média proporcional (ou média geométrica) dos extremos, pois, por exemplo:
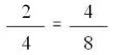
Sendo assim, é possível perceber que a média proporcional entre 2 e 8 é 4, já que:
8.2 = 4.4
Grandezas Diretamente Proporcionais
É um tipo de proporção que envolve duas grandezas e quando uma delas é aumentada a outra também aumenta na mesma proporção ou diminuindo uma delas a outra também diminui na mesma proporção. Sendo duas grandezas A e B diretamente proporcionais, então, a relação estabelecida entre elas é: A/B = K ou A = B.K.
Grandezas Inversamente Proporcionais
É o tipo de proporção que envolve duas grandezas e quando uma delas aumenta a outra diminui na mesma proporção ou diminuindo uma delas a outra aumenta na mesma proporção. Sendo duas grandezas A e B inversamente proporcionais, então, a relação estabelecida entre elas é: A.B = K ou A = K/B
REFERÊNCIAS
BARUK, Stella. Dictionnaire des Mathématiques Élémentaires. Éditeur : Seuil, 1995
http://www.fau.ufrj.br/apostilas/aforma/CAP5.pdf
http://www.mathsisfun.com/algebra/proportions.html
http://www.math.com/school/subject1/lessons/S1U2L2GL.html
http://www.les-mathematiques.net/phorum/read.php?2,4239
http://www.cnrtl.fr/lexicographie/proportionnel
Por: Anderson Andrade Fernandes