A regra de três simples é usada para se conhecer uma quantidade que forma uma proporção com outras quantidades conhecidas de duas grandezas. Existem regras de três diretas e inversas.
A regra de três é uma técnica que permite resolver problemas que envolvem duas grandezas relacionadas, para os quais determinamos o valor de uma das grandezas, conhecendo-se os outros três valores envolvidos.
Como aplicar a regra de três simples
- 1º passo – identificar as grandezas envolvidas, descobrir se a relação entre elas é direta ou inversamente proporcional;
- 2º passo – montar a tabela com as proporções;
- 3º passo – montar a proporção e resolvê-la.
Exemplo 1
Se quatro latas de refrigerante custam R$ 6,00, quanto custarão nove latas do mesmo refrigerante?
1º passo:
- as grandezas envolvidas são: preço e quantidade de latas de refrigerante;
- ao aumentar a quantidade de refrigerante, haverá aumento no custo; isto é, as duas grandezas são diretamente proporcionais.
2º passo:
3º passo: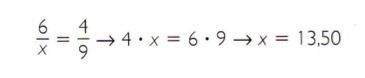
Portanto, serão pagos R$ 13,50 pelas nove latas de refrigerante.
Este exemplo também pode ser resolvido pelo processo de redução à unidade, visto anteriormente.
Calcular o preço de uma lata: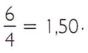 
Isso significa que cada lata de refrigerante custa R$ 1,50.
Portanto, para calcular o custo das nove latas, basta multiplicar o valor unitário por nove. Ou seja, 1,50 • 9 = 13,50.
As nove latas de refrigerante custarão R$ 13,50.
Exemplo 2
Um arquivo de 6 MB foi “baixado” a uma velocidade média de 120 kB por segundo. Se a velocidade de download fosse de 80 kB por segundo, quanto desse mesmo arquivo teria sido “baixado” no mesmo intervalo de tempo?
1º passo:
- as grandezas envolvidas são: velocidade de download e tamanho do arquivo:
- ao diminuir a velocidade de download, no mesmo intervalo de tempo, são “baixados” menos dados: portanto, são grandezas diretamente proporcionais.
2º passo: 
3º passo:
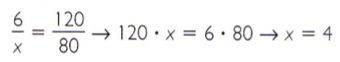
Portanto, no mesmo intervalo de tempo, será possível “baixar” 4 MB do arquivo.
Pode-se resolver esse exercício por meio do método da redução à unidade.
Calcular o tamanho do arquivo que é possível “baixar” com velocidade de 1 kB por segundo.
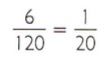
Com velocidade de 1 kB por segundo, pode-se, no mesmo intervalo de tempo, “baixar”
MB do mesmo arquivo.
Então, para saber quanto do arquivo é possível “baixar” com velocidade de 80 kB, basta multiplicar o resultado por 80.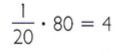
Portanto, com uma velocidade de 80 kB por segundo, pode-se “baixar” 4 MB de dados do mesmo arquivo.
Exemplo 3
Um mapa foi confeccionado na escala 1 : 500000. Se a distância entre duas cidades nesse mapa é de 5 cm, qual a distância real entre elas?
1º passo:
As duas grandezas envolvidas são: distância no mapa e distância real.
Se a escala é de 1 : 500000, isso significa que cada 1 cm no mapa corresponde a 500000 cm em valor real. Ao aumentar a medida no mapa, aumenta-se o valor real. Portanto, as duas grandezas são diretamente proporcionais.
2º passo
3º passo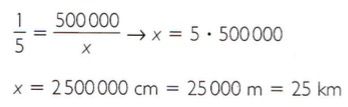
Portanto, a distância que separa as duas cidades é de 25 km.
Exemplo 4
Um motorista fez uma viagem entre duas cidades em 6 horas, mantendo uma velocidade média de 60 km/h. Se, na volta, percorrendo a mesma estrada, a sua velocidade média foi de 80 km/h, qual foi a duração da viagem?
1º passo:
As duas grandezas envolvidas são: velocidade média durante a viagem e tempo gasto. Ao aumentar a velocidade média, a mesma distância é percorrida em um intervalo de tempo menor. Portanto, as grandezas são inversamente proporcionais.
2º passo:
3º passo:
Por serem grandezas inversamente proporcionais, o produto entre os valores será constante.
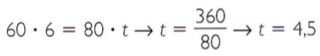
Portanto, a viagem será feita em 4,5 h = 4h30min.
Exemplo 5
A concentração de um soluto é a razão entre a massa dessa substância e o volume do solvente. Considere que foram dissolvidos cinco gramas de sal de cozinha em 500 mL de água.
Ao acrescentar 250 mL de água, qual será a nova concentração do sal?
Calcule a concentração inicial: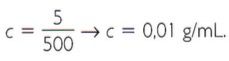
1º passo:
As duas grandezas envolvidas são: concentração da substância e volume de água.
Em uma fração, quando o denominador aumenta, mantendo-se constante o numerador, a fração diminui.
Então, à medida que o volume de água aumenta, a concentração da substância diminui. Portanto, são grandezas inversamente proporcionais.
2º passo:
3º passo:
Por serem grandezas inversamente proporcionais, o produto entre os seus valores deverá ser constante.
Portanto, a nova concentração do sal de cozinha na água é de, aproximadamente, 0,007 g/mL.
Por: Paulo Magno da Costa Torres
