1. Resistores
Os resistores são caracterizados por uma grandeza física que mede a a posição, oferecida pelas partículas que os constituem, à passagem de corrente elétrica.
Seja o resistor representado no trecho de circuito AB, onde se aplica uma ddp U entre seus extremos e se estabelece uma corrente de intensidade i.
A 0———————/\/\/\/\/\/\———————0 B
-> i
Define-se como resistência elétrica R do resistor o quociente da ddp U entre seus terminais pela corrente i que o atravessa.
U
R = —
i
Observações:
De uma maneira em geral, a resistência elétrica R do resistor depende tanto da sua natureza e das suas dimensões como da sua temperatura. Portanto, em geral, a resistência de um resistor é uma grandeza variável.
Os fios metálicos que fazem parte de um circuito elétrico também funcionam como resistores, ou seja, eles também oferecem uma certa resistência à passagem de corrente. Ocorre, porém, que normalmente sua resistência é muito pequena, quando comparada com a resistência dos demais resistores envolvidos no circuito, podendo ser considerada desprezível. Nesses casos, sua representação é uma linha contínua.
A 0————————————————————0
-> fio condutor (resistência desprezível)
O resistor é um ente concreto e a resistência elétrica é um ente abstrato.
1.1. Primeira Lei de Ohm
Numa experiência, Georg Simon Ohm aplicou, sucessivamente, as tensões U1, U2, U3, …, Un entre os terminais de um resistor e obteve, respectivamente, as correntes i1, i2, i3, …, in.
Observou-se que esses valores são relacionados da seguinte forma:
U1 U2 U3 Un U
— = — = — = … = — = — = R = constante
i1 i2 i3 in i
A intensidade da corrente elétrica que percorre um resistor é diretamente proporcional à tensão entre seus terminais.
Essa lei de Ohm é valida apenas para alguns resistores, que foram determinados resistores ôhmicos.
Os resistores para os quais a resistência não se mantém constante são denominados resistores não-ôhmicos.
A unidade de resistência elétrica no SI é ohm (Ω) definido por:
1 volt
———— = 1 ohm = 1 Ω
1 ampère
É usual a utilização de:
1 megaohm -> M Ω = 10 ⁶ Ω
1 microohm -> µ Ω = 10 – ⁶ Ω
1.2 Potência Dissipada
Consideramos um resistor de resistência R submetido á tensão U e percorrido por uma corrente i.
U
<————————————–——————>
↕ -> i R ↕
A 0—————/\/\/\/\/\/\/\/\—————0 B
Sabemos, da Eletrostática, que o trabalho (T) para deslocar uma quantidade de carga deltaQ do ponto A para o ponto B é dado por:
T = deltaQ . (VA — VB)
T = deltaQ . U
Dividindo-se ambos os membros pelo intervalo de tempo delta t decorrido para carga delta Q transferir-se de A para B, vem:
T delta Q
—— = —— . U
delta t delta t
T
Mas: —— = P (Potência)
delta t
delta Q
——— = i
delta t
Então, substituindo-se: P = U.i
A Potencia dissipada num trecho AB de um condutor qualquer é dada pelo produto da ddp U, entre os pontos a e B, pela intensidade da corrente elétrica entre esses pontos.
O termo dissipar é usado no sentido de consumir; logo, a quantidade de energia elétrica consumida no resistor, durante certo intervalo de tempo delta t vale: T = P. delta t
Como, pela definição de resistor, toda a energia consumida por ele é transformada em energia térmica, sendo dissipada sob a forma de calor, temos:
T = Q
Para se obter o calor Q em calorias, deve-se considerar a expressão:
T = J.Q (onde J = 4,18).
Uma unidade muito utilizada é o quilowatt-hora (kWh). Um kWh é a quantidade de energia com potencia de 1 kW, que é transformada no intervalo do tempo de 1h.
1.3 Segunda Lei de Ohm
Consideramos um fio condutor de comprimento ℓ e seção transversal de área S.
Através de experiências, Ohm verificou que a resistência elétrica R é diretamente proporcional ao comprimento do fio condutor e inversamente proporcional à área de sua seção transversal.
Em que: ρ é a resistividade elétrica.
ℓ
R = ρ —
S
A constante de proporcionalidade ρ depende da natureza do material condutor, da temperatura e das unidades adotadas.
2. Geradores – Força Eletromotriz
Um gerador transforma uma modalidade qualquer de energia em energia elétrica. As cargas elétricas da corrente que atravessa o gerador chegam pelo polo de potencial mais alto, polo positivo.
É considerado gerador ideal aquele que consegue transferir às cargas que o atravessam toda energia elétrica transformada.
A diferença de potencial entre os polos de um gerador ideal é chamado força eletromotriz (f.e.m.). A f.e.m. é representada pela letra E, e sendo uma ddp sua unidade de medida é volt.
2.1. Gerador Ideal
Na pratica, quando a corrente elétrica atravessa o gerador ela o faz através de condutores, que oferecem uma certa resistência à sua passagem. A essa resistência denominamos resistência internado gerador (r).
A diferença de potencial U entres os polos de um gerador real é igual à diferença entre sua f.e.m. E e a queda de tensão r . i causada pela passagem da corrente i pelo gerador de resistência interna r.
Equação do gerador: U = E – r.i
2.2. Rendimento de um Gerador
Multiplicando a equação do gerador U = E – r.i pela corrente i, temos U.i = E.i-r.i². Lembrando que a potencia elétrica é dada por P = U.i, temos:
Pu = Pt – Pd, onde:
Pu = U . i: potência útil que o gerador coloca à disposição do circuito.
Pt = E . i: potência total do gerador.
Pd = r . i²: potência dissipada pela resistência interna.
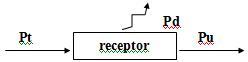
3. Receptores – Força Contra-Eletromotriz
Quando um gerador estabelece uma diferença de potencial U entre os terminais de um receptor, ela se divide da seguinte forma: uma parte desta E’, chamada de força contra eletromotriz (f.c.e.m.), é utilizada de forma util e a outra parte, que representa a queda de tensão r’ . i decorrente da passagem da corrente elétrica, é dissipada sob forma de calor.

Assim, a equação do receptor é: U = E’ + r . i
Num receptor as cargas elétricas chegam ao polo positivo, sofrem uma perda de energia na realização de um trabalho útil e saem, pelo polo negativo com um potencial elétrico menor.
3.1. Rendimento de um Receptor
Multiplicando a equação do receptor pela corrente i, temos:
U = E’ + r’i -> Ui = E’i +r . i²
Pt = Pu + Pd
Em que:
Pt = Ui: potencia total consumida pelo receptor.
Pu = E’i: potencia útil.
Pd = r’ . i²: potencia dissipada pela resistência interna do receptor.
O rendimento elétrico de um receptor é a relação entre a potência útil e a potência total consumida pelo receptor:
Pu
η = —
Pt
Mas,
Pu = E’ . i
Pt = U . i
Conclusão
Tiramos a conclusão neste estudo que, resistores, geradores e receptores tem muita importância para com a população, pois são eles que colaboram com a produção de energia elétrica que trazem luz para as pessoas em suas casas.
Bibliografia
1 BONJORNO, Regina,José Roberto, Valter e RAMOS, Clinton Marcico. Física 2º Grau. São Paulo: FTD, 1988.
Por: Diego Bortoli