Movimento Circular

Assim como qualquer outro tipo de movimento em física, o movimento circular uniforme possui algumas peculiaridades.

A mecânica clássica é área da física que estuda o movimento em suas mais variadas formas. Assim como toda teoria em física, ela possui algumas leis que devem ser respeitadas. O grande desafio da mecânica é buscar através de suas leis e artifícios matemáticos a equação da trajetória de um corpo. A trajetória pode ser entendida como sendo a união de vários pontos sucessivos em que o movimento evolui. Para deixar essa ideia de trajetória mais concreta, um esquema foi montado abaixo:

Agora conhecido a definição de trajetória, pode-se pensar em movimentos circulares.

A grande característica dos movimentos circulares é a presença da força centrípeta que consequentemente gera uma aceleração centrípeta.

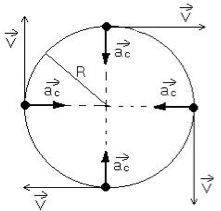
Os movimentos circulares podem ser:

1 – Movimento circular uniforme (MCU)

Nesse caso, o movimento possui como característica:

1. Sua trajetória é de forma circular
2. O módulo de sua velocidade é sempre mantido constante.

OBSERVAÇÃO: visto que como a velocidade é uma grandeza vetorial e apenas seu módulo é mantido constante, logo sua direção e seu sentido variam e então é aqui que surge a aceleração centrípeta.

As equações matemáticas para a análise desse movimento devem ser funções do ângulo referente ao movimento. As equações são basicamente as mesmas do movimento retilíneo uniforme fazendo apenas as conversões de grandezas lineares para grandezas angulares.

a) Velocidade angular:

A velocidade angular é formulada como:

ω = ΔΘ/Δt

onde: ω = velocidade angular
ΔΘ = deslocamento angular
Δt = variação no tempo

Outra forma para calcular a velocidade angular é relacionando-a com a velocidade linear de forma que:

v = ωR

OBSERVAÇÃO: O espaço angular tem como unidade no sistema internacional o grau. Já a velocidade angular tem como unidade o radiano por segundo (rad/s).

b)  Aceleração centrípeta:

A aceleração centrípeta aponta sempre para o centro da circunferência e é calculada da forma:

ac = v²/R

ou

ac = ω²R

onde: ac = aceleração centrípeta
v = velocidade linear
R = raio da trajetória
ω = velocidade angular

c) Equação horária da posição:

Θ = Θo + ωt

Onde: Θ = posição angular final
Θo = posição angular inicial
ω = velocidade angular

2 – Movimento circular uniformemente variado (MCUV)

Nesse caso, o movimento possui como característica:

1. Sua trajetória é sempre circular
2. Sua velocidade varia o módulo, direção e sentido.
3. Presença da aceleração angular definida como:

α = Δω/Δt

onde: Δω = variação da velocidade angular
α = aceleração angular
Δt = variação do tempo

Como dito, as equações matemáticas para a análise desse movimento devem ser funções do ângulo referente ao movimento. As equações são basicamente as mesmas do movimento retilíneo uniformemente variado fazendo apenas as conversões de grandezas lineares para grandezas angulares.

a) equação horária da posição:

ω = ωo + αt

onde: ω = velocidade angular final
ωo = velocidade angular inicial
α = aceleração angular

2 – a equação de Torricelli para o (MCUV) é:

ω² = ωo² – 2αΔΘ

onde: ω = velocidade angular final
ωo = velocidade angular inicial
α = aceleração angular
ΔΘ = variação do espaço angular

Por: Luíz Guilherme Rezende Rodrigues

Veja também:

• Exercícios sobre Movimentos Circulares
• Cinemática Vetorial – Exercícios
• Movimento Curvilíneo e Características
• Impulso e quantidade de movimento – Exercícios
• Movimento Retilíneo