Para operar cálculos com exatidão, precisa-se dos números irracionais, além dos racionais. A união de ambos os conjuntos forma o conjunto dos números reais.
O conjunto dos números reais
O conjunto dos números reais, representado por R, é formado pelos números racionais e irracionais.
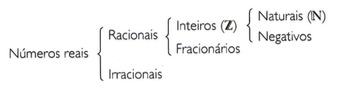
Exemplo:
O menor conjunto numérico ao qual pertence cada um dos seguintes números é:
- a) -3————► é um inteiro negativo; conjunto Z
- b) 0,03333…—-► é um decimal periódico misto; conjunto Q
- c) 14————–► é um número natural; conjunto N
- d)
———-► é um número irracional; conjunto I
Ordem dos números reais
Para ordenar números reais, é conveniente colocá-los na forma decimal e comparar suas expressões.
Exemplo:
Comparar os números reais, √10 
e 3,1415.
A expressão decimal de cada um deles é
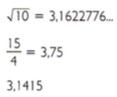
Portanto, é possível ordená-los da seguinte maneira;
Representação dos números reais
Já se mostrou como representar frações na reta numérica e, portanto, como representar qualquer número racional.
Para representar um número irracional, podem-se usar dois métodos: a representação exata e a representação por aproximação.
Representação exata
E um método utilizado para representar raízes.
Consiste em construir um triângulo retângulo cuja hipotenusa meça a raiz que se deseja representar.
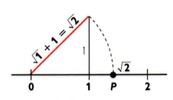
O ponto P representa 
Representação por aproximação
Consiste em ir tomando aproximações decimais por excesso e por falta do número que se quer representar.
Representar uma aproximação de 
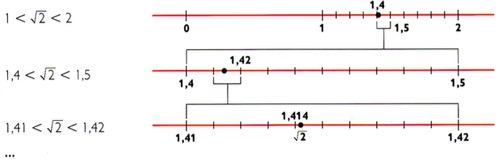
Se fosse possível representar todos os números racionais e irracionais sobre a reta numérica, se observaria que não sobram espaços vazios livres entre os números, ou seja, os números reais ocupam por completo a reta numérica. Por isso, a reta numérica é chamada também de reta real.
Por: Osvaldo Shimenes Santos
