Os números racionais são todos os números que podem ser expressos em forma de fração.
Os números irracionais são aqueles com uma quantidade ilimitada de algarismos não-periódicos e que não podem ser expressos como fração.
Números racionais
O conjunto Q dos números racionais é formado por todos aqueles números que podem ser expressos na forma de fração a/b, em que o e b são números inteiros e b é diferente de 0.
Ao calcular a expressão decimal de um número racional, dividindo o numerador pelo denominador, obtêm-se números inteiros ou decimais.
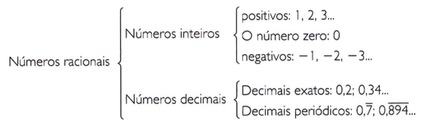
Os números decimais podem ter:
- Um número finito de algarismos, número decimal exato, se os únicos divisores do denominador forem 2 ou 5.
- Um número infinito de algarismos, que se repetem de forma periódica.
- a partir da vírgula, decimal periódico simples, se 2 ou 5 forem divisores do denominador;
- a partir do algarismo dos décimos, centésimos…, decimal periódico composto, se entre os divisores do denominador estiver o 2 ou o 5 e houver, além desses, outros divisores.
Reciprocamente, qualquer número decimal exato ou periódico pode ser expresso na forma de fração.
Exemplo:
Expressar na forma de fração os seguintes números decimais:
Representação canônica de um número racional
Dada uma fração, existem infinitas frações equivalentes a ela.
é o conjunto das frações equivalentes à fração irredutível 
.
Um conjunto de frações equivalentes representa um único número racional.
Cada fração do conjunto é um representante do número racional, e a fração irredutível com denominador positivo é o representante canônico.
Assim, o número racional é formado pela fração e todas as suas equivalentes:
Todas elas são representantes do número racional .
Portanto,e o representante canônico.
Números irracionais
O conjunto I dos números irracionais é formado pelos números que não podem ser expressos em forma de fração. São números cuja expressão decimal tem um número infinito de algarismos que não se repetem de forma periódica.
Existem infinitos números irracionais: 
é irracional e, em geral, é irracional qualquer raiz não-exata, como 
também é irracional e podem-se gerar números irracionais combinando seus algarismos decimais; por exemplo, o = 0,010010001… ou b = 0,020020002…
Com esses números, podem-se calcular soluções em equações do segundo grau (x2 = 2 —> x = que não é racional), o comprimento de uma circunferência (C = 2r, em que não é racional) etc.
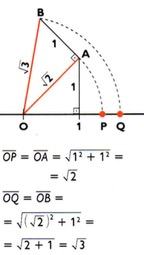
Os números irracionais do tipo 
, sendo o um número natural, podem ser representados de maneira exata na reta numérica utilizando-se o Teorema de Pitágoras; para os demais, calcula-se sua expressão decimal e representa-se uma aproximação.
Exemplo:
Verificar se cada um dos seguintes números é racional ou irracional.
a) 
; portanto, é um numero racional.
b) 
é um número irracional; se fosse um número racional poderia ser representado na forma de uma fração irredutível: 
, em que a e b não têm fatores comuns.
que significa que a2 é divisível por b2, ou seja, têm divisores comuns, contradizendo o fato de que a fração 
seja irredutível. Demonstra-se essa afirmação por absurdo.
Por: Osvaldo Shimenes Santos
