Potência é uma forma simplificada de expressar uma multiplicação em que todos os fatores são iguais. A base são os fatores da multiplicação e o expoente é o número de vezes que a base é multiplicada.
Seja a um número real e n um número natural maior que 1. Potência de base a e expoente n é o produto de n fatores iguais a a. Representa-se a potência pelo símbolo an.
Assim:
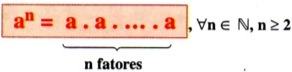
Para expoente ZERO e expoente UM, adotam-se as seguintes definições: a0 = 1 e a1 = a
Seja a um número real, não-nulo, e n um número natural. A potência de base a e expoente negativo -n é definida pela relação:
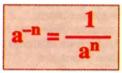
RESOLVENDO OS EXERCÍCIOS:
1. Calcular: 23; (-2)3 ;-23
Resolução
a) 23 = 2 . 2 . 2 = 8
b) (- 2)3 = (- 2) . (- 2) . (- 2) = – 8
c) -23 = -2.2.2 = -8
Resposta: 23 = 8; (- 2)3 = – 8; – 23 = – 8
2. Calcular: 24; (- 2)4; – 24
Resolução
a) 24 = 2 .2. 2. 2 = 16
b) (-2)4 = (-2).(-2).(-2).(-2) = 16
c) -24 = -2.2.2.2=-16
Resposta: 24 = 16; (- 2)4 = 16; – 24 = -16
3. Calcular: ![]()
Resolução
![]()
b) (0,2)4 = (0,2) . (0,2) . (0,2) . (0,2) = 0,0016
c) (0,1)3 = (0,1). (0,1) .(0,1) = 0,001
Respostas: ![]()
4. Calcular: 2-3; (- 2)-3; – 2-3
Resolução
![]()
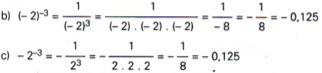
Resposta: 2-3 = 0,125; (- 2)-3 = – 0,125; – 2′3 = – 0,125
5. Calcular: 10-1; 10-2; 10-5
Resolução

Resposta: 10-1 = 0,1; 10-2 = 0,01; 10-5 = 0,00001
6. Verificar que: 0,6 = 6. 10-1; 0,06 = 6. 10-2; 0,00031 = 31 . 105; 0,00031 = 3,1 . 10-4

Propriedades da Potenciação
Sendo a e b números reais, m e n números inteiros, valem as seguintes propriedades:
a) Potências de mesma base
Para multiplicar, mantém-se a base e somam-se os expoentes.
Para dividir, mantém-se a base e subtraem-se os expoentes.

b) Potências de mesmo expoente
Para multiplicar, mantém-se o expoente e multiplicam-se as bases.
Para dividir, mantém-se o expoente e dividem-se as bases.
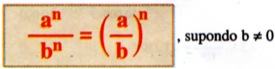
Para calcular a potência de outra potência, mantém-se a base e multiplicam-se os expoentes.
Observações
Se os expoentes forem inteiros negativos, as propriedades também valem.
Lembrar, porém, que nestes casos as bases devem ser diferentes de zero.
As propriedades do item (2) têm a finalidade de facilitar o cálculo. Não é obrigatório o seu uso. Devemos usá-las quando for conveniente.
Exemplos
I) Calcular o valor de 23 . 22 sem usar a propriedade, 23 . 22 = 2 . 2 . 2 . 2 . 2 = 8 . 4 = 32, dá praticamente o mesmo trabalho que obter este valor utilizando a propriedade, 23 . 22 = 23+2 = 25 = 2 . 2 . 2 . 2 . 2 = 32
II) Calcular, entretanto, o valor de 210 ÷ 28 sem usar a propriedade,
210 ÷ 28 = (2.2.2.2.2.2.2.2.2.2) + (2.2.2.2.2.2.2.2) = 1024 / 256 = 4,
é, com certeza, muito mais trabalhoso do que simplesmente usar a propriedade 210 ÷ 28 = 210 -8 = 22 = 4
RESOLVENDO OS EXERCÍCIOS:
7. Verificar, usando a definição de potência, que a3 . a4 = a3+4 = a7.
Resolução
a3 . a4 = (a . a . a). (a . a . a . a) = a . a . a . a . a . a . a = a7
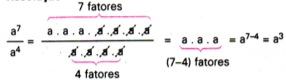
8. Verificar, usando a definição de potência, que ![]() para a ? 0
para a ? 0
Resolução
9. Verificar, usando a definição de potência, que a3 . b3 = (a . b)3.
Resolução
a3. b3 = (a . a . a). (b . b . b) = (a . b). (a . b). (a . b) = (a . b)3.
10. Verificar que a23 = a8.
Resolução
a23 = a2 . 2 . 2 = a8
11. Sendo n ? N, mostrar que 2n + 2n+1 = 3 . 2n
Resolução
2n + 2n+1 = 2n + 2n . 2 = (1 + 2) . 2n = 3 . 2n
12. Verificar, usando a definição de potência, que ![]() para b ? 0
para b ? 0
Resolução
![]()