A regra de três usada para resolver um problema relacionado a duas grandezas proporcionais é chamada regra de três simples. Se houver mais de duas grandezas proporcionais, será chamada de regra de três composta.
Quando se trabalha com mais de duas grandezas relacionadas proporcionalmente entre si, verifica-se um problema de proporcionalidade (regra de três) composta. Para resolvê-lo é necessário determinar o tipo de proporcionalidade existente entre a incógnita e o resto das grandezas relacionadas.
Exemplo 1
Com o uso de um computador foi possível copiar 4 GB de imagens e sons em 15 minutos. Para copiar 12 GB de imagens e sons semelhantes aos gravados, utilizando 2 computadores idênticos ao anterior e funcionando simultaneamente, quanto tempo será necessário?
O primeiro passo é ver o tipo de proporcionalidade existente entre a grandeza que contém a incógnita (tempo) e as outras duas grandezas.
- Quanto maior o tempo de funcionamento do computador, maior será a quantidade de informação a ser gravada. Portanto, as grandezas tempo e quantidade de imagens e sons são diretamente proporcionais.
- Quanto mais computadores estiverem em funcionamento, menos tempo será necessário para copiar os dados. Portanto, as grandezas tempo e número de computadores são inversamente proporcionais.
Para resolver este problema, multiplicar os quocientes das quantidades quando as grandezas são diretamente proporcionais, multiplicar pelos seus inversos se a proporcionalidade for inversa e igualar ao quociente das quantidades da incógnita.
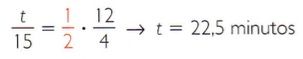
Para gravar os 12 GB de imagens e sons, com dois computadores, serão necessários 22,5 minutos.
Exemplo 2
Cinco fotocopiadoras levam 6 minutos para fazer 600 fotocópias. Ao colocar 7 fotocopiadoras idênticas às anteriores para fazer 1 400 fotocópias, quantos minutos serão necessários?
Nesse caso, há três grandezas proporcionais: o número de fotocopiadoras, o número de fotocópias e o número de minutos.
Como estão relacionadas mais de duas grandezas, diz-se que existe uma regra de três composta.
O primeiro passo é averiguar que tipo de proporcionalidade existe entre a grandeza da incógnita (número de minutos) e as outras duas grandezas:
- Mais copiadoras, menos minutos. Proporcionalidade inversa.
- Mais fotocópias, mais minutos Proporcionalidade direta.
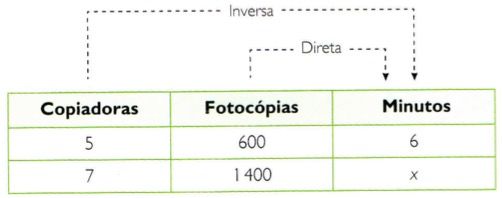
Para resolver o problema, reduz-se à unidade, isto é, calcula-se o número de minutos que uma copiadora demora para fazer uma cópia.
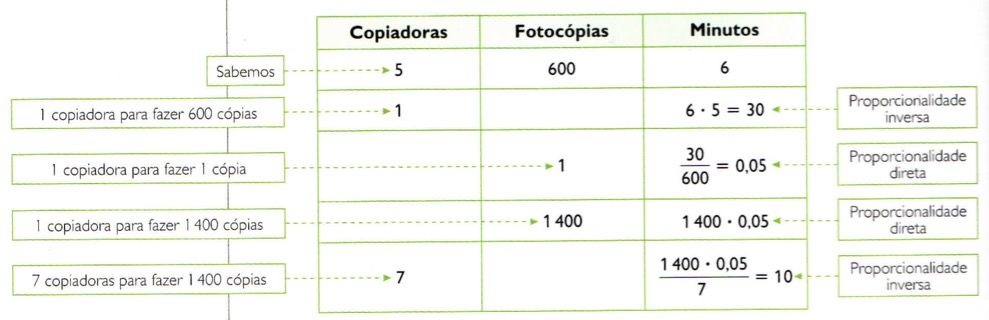
Sete fotocopiadoras levarão 10 minutos para fazer 1 400 fotocópias.
Exemplo 3
Vinte homens trabalharam durante 6 dias para estender 400 metros de cabo, trabalhando 8 horas por dia. Quantas horas por dia terão de trabalhar 24 homens durante 14 dias para estender 700 metros de cabo?
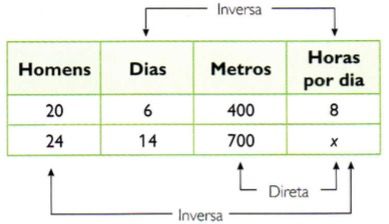Resolver o problema escrevendo as grandezas e seus valores e analisando a relação de proporcionalidade existente entre cada grandeza e a grandeza da incógnita.
Quanto mais homens, menos horas diárias (inversa); quanto mais dias, menos horas diárias (inversa); e quanto mais horas diárias, mais metros (direta).
Multiplicar os quocientes das quantidades das grandezas conhecidas, colocando seus inversos nos casos de proporcionalidade inversa e igualando ao quociente das quantidades da incógnita.
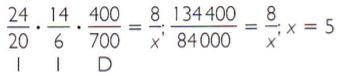
Os 24 homens trabalharão 5 horas por dia durante 14 dias para estender 700 metros de cabo.
Por: Paulo Magno da Costa Torres
