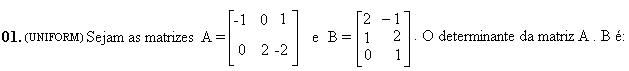
a) 64
b) 8
c) 0
d) -8
e) -64
02. Para que o determinante da matriz
1+a -1
3 1-a
seja nulo, o valor de a deve ser:
a) 2 ou -2
b) 1 ou 3
c) -3 ou 5
d) -5 ou 3
e) 4 ou -4
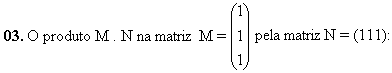
a) não se define;
b) é uma matriz de determinante nulo;
c) é a matriz identidade de ordem 3;
d) é uma matriz de uma linha e uma coluna;
e) não é matriz quadrada.
04. Sabendo-se que o determinante associado à matriz:
1 -11 6
-2 4 -3
-3 -7 2
é nulo, concluímos que essa matriz tem:
a) duas linhas proporcionais;
b) duas colunas proporcionais;
c) elementos negativos;
d) uma fila combinação linear das outras duas filas paralelas;
e) duas filas paralelas iguais.
05. (UESP) Se o determinante da matriz
p 2 2
p 4 4
p 4 1
é igual a -18, então o determinante da matriz
p -1 2
p -2 4
p -2 1
é igual a:
a) -9
b) -6
c) 3
d) 6
e) 9
06. (UESP) Se o determinante da matriz:
2 1 0
k k k
1 2 -2
é igual a 10, então o determinante da matriz:
2 1 0
k+4 k+3 k-1
1 2 -2
é igual a:
a) 7
b) 8
c) 9
d) 10
e) 11
07. Calcular o determinante da matriz:
1 5 2
4 8 3
1 2 -1
Aplicando o Teorema de Laplace e utilizando a 3º coluna.

a) 2
b) 1
c) -1
d) -2
e) 3
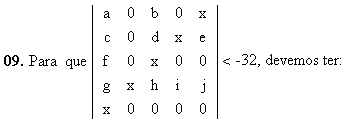
a) x > 2
b) 0 < x < 5
c) x < -2
d) x > 5
e) 1 < x < 2
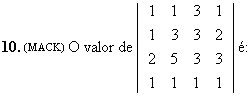
a) -4
b) -2
c) 0
d) 1
e) 1131
Respostas:
| 01. D | 02.A | 03. B | 04. D |
| 05. E | 06. C | 07. det M = 21 | |
| 08. D | 09. C | 10. C |
Veja os artigos sobre: Determinantes e Matrizes.