Ao realizar-se operações entre os elementos de uma matriz quadrada, associa-se um número chamado determinante da matriz. Representa-se como det A o determinante da matriz A e os parênteses, colchetes ou barras duplas são substituídos por barras simples.
Tomando como exemplo a matriz A =  , que pode também ser expressa entre colchetes ou barras duplas, seu determinante será representado como det A=
, que pode também ser expressa entre colchetes ou barras duplas, seu determinante será representado como det A=
Determinante de matriz de ordem 1
Uma matriz quadrada de ordem 1 apresenta apenas um elemento: o valor do seu determinante é o próprio valor desse único elemento.
Exemplo:
Determinante de matriz de ordem 2
Para obter o valor do determinante de uma matriz quadrada de ordem 2, é preciso calcular a diferença entre o produto dos elementos da diagonal principal e da diagonal secundária.
Exemplo:
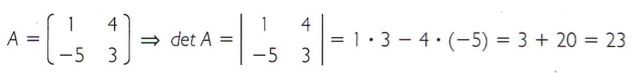
Determinante de matriz de ordem maior ou igual a 3
Existem dois métodos para o cálculo do determinante de matrizes cuja ordem é maior ou igual a 3. O primeiro, mais aconselhável para ordens próximas de 3, é a regra de Sarrus. O segundo, mais geral, é o cálculo por meio do teorema de Laplace.
Regra de Sarrus
Tomando uma matriz A de ordem 3, calcula-se o seu determinante procedendo da seguinte maneira:
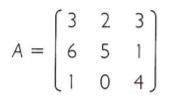 1. Copiar ao lado da matriz suas duas primeiras colunas.
1. Copiar ao lado da matriz suas duas primeiras colunas.
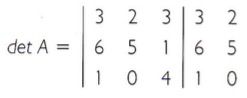 2. Multiplicar os elementos da diagonal principal, realizando o mesmo procedimento para suas paralelas à direita.
2. Multiplicar os elementos da diagonal principal, realizando o mesmo procedimento para suas paralelas à direita.
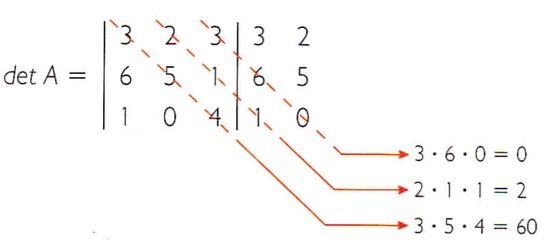
3. Multiplicar os elementos da diagonal secundária, realizando o mesmo procedimento para suas paralelas à direita.
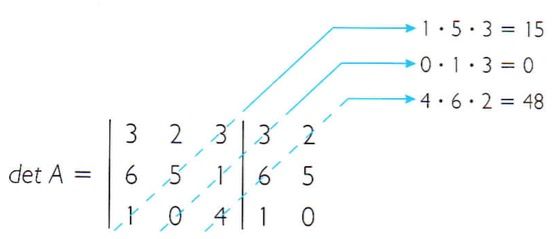 4. Subtrair as somas dos produtos obtidos nos passos 2 e 3, nessa ordem, assim:
4. Subtrair as somas dos produtos obtidos nos passos 2 e 3, nessa ordem, assim:
det A = (0 + 2 + 60) – (15 + 0 + 48)
O determinante da matriz A é dado por:
det A = 62 – 63 = -1
Para matrizes cuja ordem é maior que 3, realizam-se os mesmos procedimentos, porém, no primeiro passo, deve-se copiar ao lado da matriz todas as suas colunas, exceto a última à direita.
Teorema de Laplace
O determinante de uma matriz A, de ordem n ≥ 2, é a soma dos produtos dos elementos de uma fila (linha ou coluna) pelos seus respectivos cofatores.
Antes de desenvolver esse teorema, é preciso aprender alguns conceitos necessários para usá-lo.
Matriz Reduzida
Dada uma matriz quadrada A, a matriz reduzida Aij é obtida eliminando-se a linha i e a coluna j da matriz A.
Exemplo:
Seja a matriz A =  a matriz reduzida A13 é obtida eliminando-se a primeira linha e a terceira coluna da matriz A
a matriz reduzida A13 é obtida eliminando-se a primeira linha e a terceira coluna da matriz A
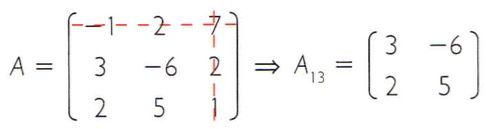
Já a matriz reduzida A21 é obtida eliminando-se a segunda linha e a primeira coluna da matriz A.
 Cofator
Cofator
Dada uma matriz quadrada A de ordem n ≥ 2, chama-se cofator de um elemento aij de A o número real Cij = (-1) i+j . ⌈Aij⌉, sendo Aij matriz reduzida obtida a partir de A eliminando-se a linha i e a coluna j.
Exemplo:
Calcular o cofator do elemento a23 da matriz A, utilizada no exemplo anterior.
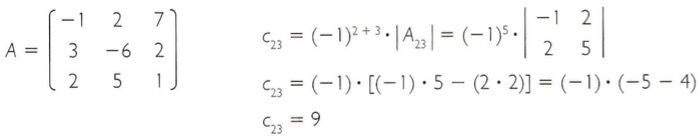
Portanto, o cofator do elemento a23 da matriz A é 9.
Calculando o determinante pelo teorema de Laplace
Para calcular o determinante da matriz A = 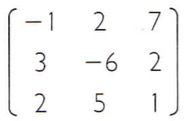 , utilizada em exemplos anteriores, e preciso:
, utilizada em exemplos anteriores, e preciso:
- escolher uma fila (linha ou coluna);
- calcular os cofatores dos elementos dessa fila;
- somar o produto de cada elemento dessa fila pelo seu respectivo
Escolhendo a terceira coluna: ![]()
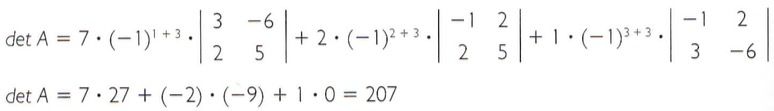
Outros teoremas importantes
Teorema de Binet
Se A e B são matrizes quadradas de mesma ordem, então vale det (A • B) = det A • det B.
Exemplo:
Nas matrizes A = 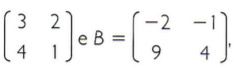 os determinantes são: det A = -5 e det B = 1.
os determinantes são: det A = -5 e det B = 1.
O produto entre as matrizes A e B é dado por.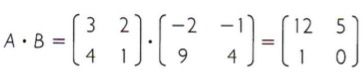
Assim, det (A • B) = 12 • 0 – 5 • 1 = -5.
Dessa forma, fica comprovado que det (A • B) = det A • det B, já que -5 = (-5) • 1.
Consequência do teorema de Binet
O determinante da matriz inversa da matriz A é igual ao inverso do determinante da matriz A.
Para comprovar isso, parte-se da definição de matriz inversa. Dela, decorre que A . A -1 = / e como det / = 1 para qualquer ordem, pode-se escrever:

Teorema de Jacobi
Dada uma matriz A de ordem qualquer, se for adicionada uma fila de A a uma fila paralela, previamente multiplicada por uma constante real, tem-se uma matriz B cujos determinantes serão os mesmos.
Exemplo:
Dadas as matrizes A 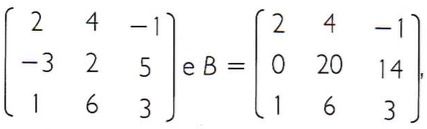
Observa-se que a segunda linha de B é a soma da segunda linha de A com o triplo da terceira linha de A.
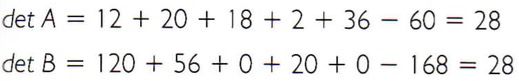
Dessa forma, conclui-se que seus determinantes são iguais.
Por: Paulo Magno da Costa Torres
Veja também:
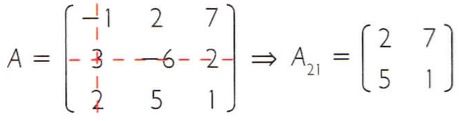 Cofator
Cofator