O uso de tabelas no cotidiano é essencial. Elas aparecem a todo momento, sem o uso de tabelas, ficar-se-ía restrito a um número menor de informações. Na Matemática, o estudo das tabelas recebe um nome especial: é o estudo das matrizes.
Uma matriz mXn é uma tabela composta por m linhas e n colunas que contém m • n elementos.
Representação de uma matriz
Uma matriz é representada por letras maiúsculas do alfabeto latino acompanhadas de sua ordem, ou seja, quantidade de linhas e colunas que possuí.
Exemplos
• A3×2 — Matriz representada pela letra A que possui 3 linhas e 2 colunas.
• B4×6 — Matriz representada pela letra B que possui 4 linhas e 6 colunas.
Cada elemento de uma matriz é representado pela mesma letra utilizada na representação da matriz, porém em letra minúscula acompanhada de seu índice, que é indicado pela posição que ocupa na matriz. Primeiro, menciona-se a linha e, posteriormente, a coluna.
Exemplos:
• a31 — Elemento da matriz A que está localizado na terceira linha e na primeira coluna.
• b15 — Elemento da matriz B que está localizado na primeira linha e na quinta coluna.
De modo geral, representa-se o elemento de uma matriz como aij, localizado na í-ésima linha e na j-ésima coluna.
Uma matriz A4×5 ainda pode ser representada da seguinte forma:

Genericamente, a matriz A é representada por A = (aij)m×n, onde 1 ≤ i ≤ m e 1 ≤ j ≤ n, com i, j ∈ N, ou ainda:
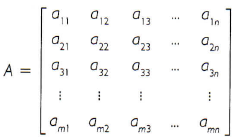
Matrizes especiais
Matriz nula
Uma matriz com todos os seus elementos iguais a zero é chamada matriz nula.
Exemplos:
A= é uma matriz nula de ordem 2×5 e pode ser indicada por A2×5.
é uma matriz nula de ordem 2×5 e pode ser indicada por A2×5.
B=  é uma matriz nula de ordem 4×3 e pode ser indicada por B4×3 .
é uma matriz nula de ordem 4×3 e pode ser indicada por B4×3 .
Matriz linha
A matriz que possui apenas uma linha é chamada matriz linha.
Exemplos:
C = [ 1 5 8 -2 ] é uma matriz linha de ordem 1×4.
D = [-3 2] é uma matriz linha de ordem 1×2.
Matriz coluna
Já a matriz que possui apenas uma coluna é chamada matriz coluna.
Exemplos:
A = 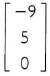 é uma matriz coluna de ordem 3×1.
é uma matriz coluna de ordem 3×1.
R = 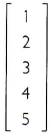 é uma matriz coluna de ordem 5×1.
é uma matriz coluna de ordem 5×1.
Matriz quadrada
Uma matriz é dita quadrada quando possui a mesma quantidade de linhas e colunas.
Exemplos:
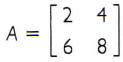 é uma matriz quadrada 2×2, ou, ainda, matriz de ordem 2. Dessa forma, podemos representá-la como A2.
é uma matriz quadrada 2×2, ou, ainda, matriz de ordem 2. Dessa forma, podemos representá-la como A2.
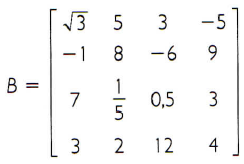 é uma matriz quadrada 4×4, ou, ainda, matriz de ordem 4.
é uma matriz quadrada 4×4, ou, ainda, matriz de ordem 4.
Também pode ser representada por B4.
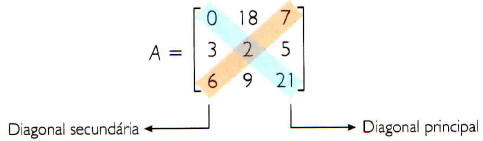
Em toda matriz quadrada, os elementos cuja posição da linha e da coluna forem iguais, ou seja, i = j, formam a chamada diagonal principal. A outra diagonal, na qual os elementos satisfazem a condição i + j = n + 1, é chamada diagonal secundária.
Na matriz A3 abaixo, indicamos as diagonais principal (ou primária) e secundária.
Matriz identidade
A matriz quadrada em que todos os elementos da diagonal principal são unitários, ou seja, iguais a 1, e os demais são nulos, ou seja, iguais a zero, recebe o nome de matriz identidade. Sua representação é sempre dada por In, sendo n a ordem da matriz.
Exemplos:
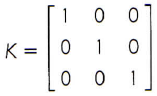 é uma matriz identidade de ordem 3 e pode ser representada por I3.
é uma matriz identidade de ordem 3 e pode ser representada por I3.
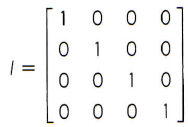 é uma matriz identidade de ordem 4 e pode ser representada por I4.
é uma matriz identidade de ordem 4 e pode ser representada por I4.
Matriz transposta
A partir de uma matriz A, é possível obter outra matriz, invertendo, ordenadamente, as linhas pelas colunas. A matriz resultante é chamada matriz transposta.
A partir de uma matriz A = (aij)m×n, pode-se definir a matriz transposta de A como sendo a matriz AT = (atij)nXm, sendo atij = aji, ou seja, as linhas da matriz AT são, ordenadamente, iguais às colunas da matriz A e as colunas da matriz AT são, ordenadamente, iguais às linhas da matriz A.
Exemplos:
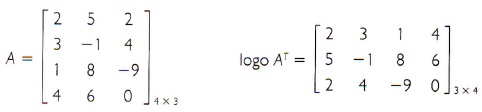
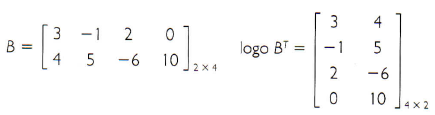
Igualdade entre matrizes
Duas matrizes A e B serão iguais se seus elementos de mesma posição forem iguais, zesde que as duas matrizes tenham a mesma ordem. Uma igualdade entre matrizes é apresentada como A = B.
Exemplos:
a) Dadas as matrizes 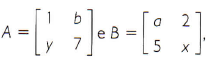 , para quais valores de a, b, x e y essas matrizes serão iguais?
, para quais valores de a, b, x e y essas matrizes serão iguais?
Note que os elementos de mesmo índice de ambas as matrizes deverão ser iguais, então:
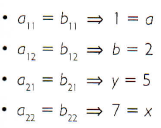
b) Dadas as matrizes 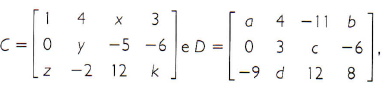 para quais valores de a, b, c, d, x, y, z e k essas matrizes são iguais?
para quais valores de a, b, c, d, x, y, z e k essas matrizes são iguais?
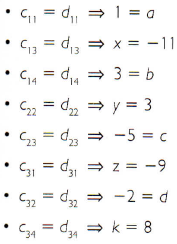
Por: Osvaldo Shimenes Santos