Aprenda a operar com matrizes, como fazer soma, subtração, multiplicação e matriz inversa.
Adição de matrizes
A adição de matrizes é definida apenas para matrizes de mesma ordem, Assim, se A = (aij)m×n e B = (bij)m×n , diz-se que a soma de A + B é dada pela matriz C = (cij)m×n, sendo cij = aij + bij para todo i compreendido no intervalo 1 ≤ i ≤ m e para todo j compreendido no intervalo 1 ≤ j ≤ n.
Exemplo:
Sejam as matrizes A e B:
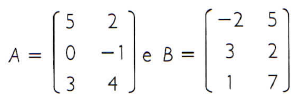
Para calcular a matriz C = A + B, basta somar seus elementos correspondentes
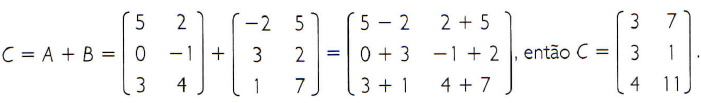
Matriz oposta
A matriz que ao ser somada a uma matriz A de ordem m X n resulta em uma matriz nula de mesma ordem é chamada matriz oposta (indicada por -A).
Exemplo:

Comprova-se isso calculando: 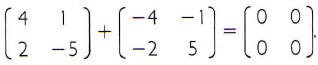
Propriedades da adição
Considerando as matrizes A, B, C e O (matriz nula), ambas de mesma ordem, valem:
- A + B = B + A (comutativa)
- (A + B) + C = A + (B + C) (associativa)
- A + 0 = 0 + A = A (existência do elemento neutro)
- A + (-A) = (-A) + A = 0 (existência do elemento oposto)
- A + C = B + C ⇔ A = B (cancelamento)
Subtração de matrizes
A subtração entre duas matrizes A e B, ambas de mesma ordem, é obtida a partir da soma da matriz A com a oposta de B, ou seja, A – B = A + (-B).
Exemplo:
Sejam as matrizes A e B:
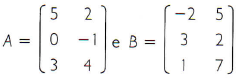
Para obter a matriz C = A – B, realiza-se os seguintes cálculos:
C = A – B = A + (-B) =
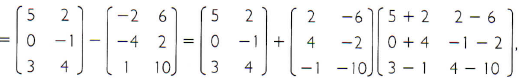 então
então
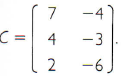
Multiplicação de um número real por uma matriz
Seja a matriz ![]() e k um número real, diz-se que k • A é uma matriz do tipo m X n, obtida a partir do produto entre k e todos os elementos da matriz A.
e k um número real, diz-se que k • A é uma matriz do tipo m X n, obtida a partir do produto entre k e todos os elementos da matriz A.
Exemplo:
Sendo A = 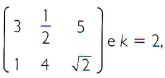 então
então
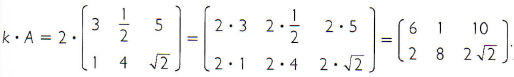
Multiplicação de matrizes
O Campeonato Brasileiro de Futebol de 2007 foi emocionante, com muitas alegrias e muitas tristezas, mas, como dizem algumas personalidades do meio esportivo, o importante é competir.
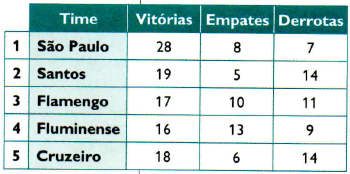
Um recurso muito utilizado para organizar a classificação dos times de qualquer torneio é uma tabela.
Ela pode conter informações como o número de vitórias, de empates e de derrotas, gols marcados, gols sofridos, mas a principal delas é a pontuação que cada time tem, já que é a tabela que dá a classificação geral.
No entanto, sabendo-se o número de vitórias, de empates e de derrotas, será possível obter-se a quantidade de pontos de cada time.
Ao lado, a tabela final do Campeonato Brasileiro de 2007, mostra os cinco primeiros colocados. Ela apresenta a quantidade de pontos com que cada um dos times terminou o campeonato.
Como para cada vitória o time marca três pontos, para cada empate, um ponto e para cada derrota não faz pontos, é possível escrever:
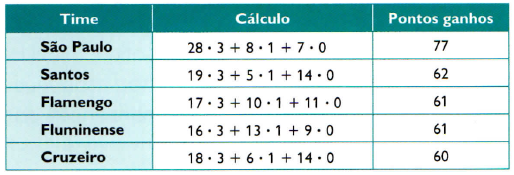
Também é possível fazer esses cálculos usando matrizes:
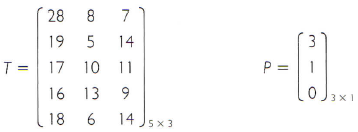
A matriz T representa as quantidades de vitórias, empates e derrotas dos cinco primeiros colocados. Cada linha representa um time diferente: São Paulo, Santos, Flamengo, Fluminense e Cruzeiro, respectivamente. Cada coluna representa a quantidade de vitórias, den_otas e empates, respectivamente. Já a matriz P representa a quantidade de pontos adquiridos caso o time ganhe, empate ou perca, respectivamente, em cada linha.
A multiplicação das matrizes T e P resulta na matriz G (pontos ganhos):
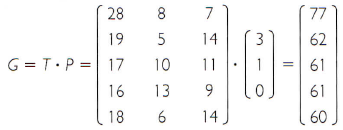
Notar que os elementos de uma linha de T são multiplicados, ordenadamente, pelos correspondentes elementos da coluna de P e, depois, os produtos são somados:
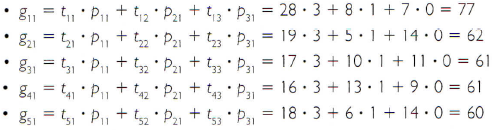
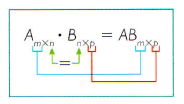
Dadas as matrizes A = (aij)m×n e B = (bij)n×p, o produto de A por B é a matriz C = (cij)m×p, na qual cada elemento cij é a soma dos produtos de cada elemento da linha i de A pelo correspondente elemento da coluna j de B.
Observação:
Dadas duas matrizes A e B, o produto AB só poderá ser obtido se o número de colunas de A for igual ao número de linhas de B. A matriz resultante terá como ordem o número de linhas de A e o número de colunas de B.
Propriedades da multiplicação
Considerando as matrizes A, B e C, valem:
- (A • B) • C = A • (B • C) (associativa)
- (A + B) • C = A • C + B • C (distributiva)
Matriz inversa
Uma matriz quadrada 8 de ordem n é a inversa da matriz quadrada A, também de ordem n, se satisfizer a seguinte condição:
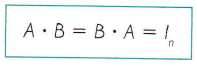 Representa-se a matriz inversa de A como sendo
Representa-se a matriz inversa de A como sendo Exemplo:
Dada a matriz A = 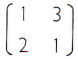 , encontrar sua matriz inversa.
, encontrar sua matriz inversa.
Se,![]() então:
então:
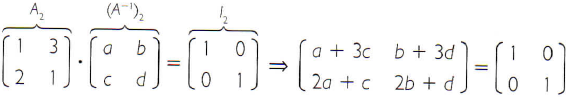
Pela igualdade de matrizes, podem-se construir os seguintes sistemas:

Portanto, conclui-se que 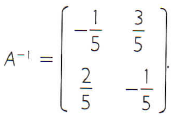
Por: Osvaldo Shimenes Santos