01. Obter a matriz A = (aij)2×2 definida por aij = 3 i – j.
02. Se A é uma matriz quadrada de ordem 2 e At sua transposta, determine A, tal que A = 2 . At.
03. (UNIV. CATÓLICA DE GOIÁS) Uma matriz quadrada A é dita simétrica se A = AT e é dita antissimétrica se AT = -A, onde AT é a matriz transposta de A. Sendo A uma matriz quadrada, classifique em verdadeira ou falsa as duas afirmações:
(01) A + AT é uma matriz simétrica
(02) A – AT é uma matriz antissimétrica
04. Se uma matriz quadrada A é tal que At = -A, ela é chamada matriz antissimétrica. Sabe-se que M é antissimétrica e:
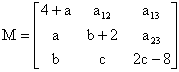
Os termos a12, a13 e a23 de M, valem respectivamente:
a) -4, -2 e 4
b) 4, 2 e -4
c) 4, -2 e -4
d) 2, -4 e 2
e) 2, 2 e 4
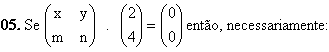
a) x = y = 0
b) x = y = m = n = 0
c) x = y e m = n
d) y = -2x e n = -2m
e) x = -2y e m = -2n
06. Na confecção de três modelos de camisas (A, B e C) são usados botões grandes (G) e pequenos (p). O número de botões por modelos é dado pela tabela:
Camisa A | Camisa B | Camisa C | |
Botões p | 3 | 1 | 3 |
Botões G | 6 | 5 | 5 |
O número de camisas fabricadas, de cada modelo, nos meses de maio e junho, é dado pela tabela:
| Maio | Junho | |
| Camisa A | 100 | 50 |
| Camisa B | 50 | 100 |
| Camisa C | 50 | 50 |
Nestas condições, obter a tabela que dá o total de botões usados em maio e junho.
RESOLUÇÃO:
07. Sobre as sentenças:
I. O produto das matrizes A3 x 2 . B2 x 1 é uma matriz 3 x 1.
II. O produto das matrizes A5 x 4 . B5 x 2 é uma matriz 4 x 2.
III. O produto das matrizes A2 x 3 . B3 x 2 é uma matriz quadrada 2 x 2
É verdade que:
a) somente I é falsa;
b) somente II é falsa;
c) somente III é falsa;
d) somente I e III são falsas;
e) I, II e III são falsas.
08. (MACK) Se A é uma matriz 3 x 4 e B uma matriz n x m, então:
a) existe A + B se, e somente se, n = 4 e m = 3;
b) existe AB se, e somente se, n = 4 e m = 3;
c) existem AB e BA se, e somente se, n = 4 e m = 3;
d) existem, iguais, A + B e B + A se, e somente se, A = B;
e) existem, iguais, AB e BA se, e somente se, A = B.
09. Sejam as matrizes:
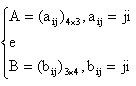
Se C = A . B, então C23 vale:
a) 3
b) 14
c) 39
d) 84
e) 258
10. (PUC) Se A, B e C são matrizes quadradas e At, Bt e Ct são suas matrizes transpostas, e igualdade falsa entre essas matrizes é:
a) (A = B) . C = A . C + B . C
b) (A + B)t = At + Bt
c) (A . B)t = At . Bt
d) (A – B)C = AC – BC
e) (At)t = A
Leia os artigos: Matrizes e Operações com Matrizes
Respostas:
01.
![]()
02.
![]()
03.
(01) verdadeira
(02) verdadeira
04. B
05. E
06.
| Maio | Junho | |
| Botões p | 500 | 400 |
| Botões G | 1100 | 1050 |
| 07. B | 08. C | 09. D | 10. C |