Estudar o espaço, as formas nele contidas, interagir com essas formas e criar a partir delas são necessidades que o ser humano tem durante toda a vida, tudo isso faz parte da geometria.
Não se sabe ao certo quando o ser humano começou a estudar Geometria. Os chineses foram os primeiros a utilizá-la no cotidiano, perto do ano 3000 a.C, mas foram os egípcios, 1500 anos depois, que contribuíram consideravelmente para o desenvolvimento dessa ciência, As constantes enchentes do rio Nilo levaram os egípcios a desenvolver uma estrutura para detê-las. Isso foi feito por meio da Geometria.
As pirâmides que construíram são outra demonstração do conhecimento que alcançaram nessa ciência. Simultaneamente aos egípcios, também os babilônios e assírios aplicaram a Geometria na Astronomia por causa de suas crenças religiosas. A partir de 600 a.C., os gregos desenvolveram ainda mais a Geometria, além de racionalizá-la e ordená-la. Gregos como Pitágoras (569-500 a.C), Aristóteles (384-322 a.C) e Euclides (330-260 a.C.) fizeram contribuições fundamentais para a Geometria.
A Geometria que estudamos hoje é conhecida como euclidiana, em homenagem ao grego Euclides, o primeiro matemático a apresentar a Geometria de forma organizada. Por quase dois séculos, todos os estudos Geométricos se basearam em seu famoso livro, “Os Elementos”.
Ponto e Reta
A geometria é construída a partir de três ideias: a ideia de ponto, reta e plano.
Podemos ter a ideia de ponto observando marcas de lápis:
Podemos ter a ideia de reta se pudermos imaginar um fio, sem começo nem fim, bem esticado:
______________________________________________
Agora, se considerarmos apenas um pedaço desse fio e o mantivermos bem esticado, temos a ideia de um segmento de reta:
_____ . _________________________________ . ________
=Para indicar retas, usamos letras minúsculas do alfabeto (a,b,c, …… r,s,t …) ou dois pontos dessas retas.Veja o segmento de reta abaixo:

Os segmentos de reta serão indicados através dos pontos que representam as extremidades desses segmentos:

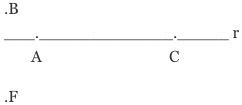
Na geometria, consideramos a reta como um conjunto de pontos. Assim, dada uma reta r, dizemos que há pontos que pertencem(A, C) e pontos que não pertencem (B, F) a essa reta.Veja:
Posições de uma Reta
As retas podem ter várias posições.
Veja agora as posições de uma reta:
*Duas retas distintas que estão em um mesmo plano e não tem ponto em comum são chamadas retas paralelas.
Plano
Observe, agora, a região externa de uma garrafa ou de uma bola, ou, ainda a parte superior de uma mesa, ou do piso de uma sala.Essas regiões nos dão ideia de superfície.
Se pudermos imaginar que é possível prolongar o tampo de uma mesa em todas as direções, teremos a ideia de plano:
Semi-Reta
Como já vimos, na geometria, a reta é considerada um conjunto de pontos. Considere um ponto A que pertence a uma reta r. Podemos dizer que esse ponto A separa a reta em dois conjuntos de pontos. Cada um desses conjuntos de pontos é denominado semi-reta.
O ponto A é chamado origem das semi-retas.
Na reta abaixo, o ponto A divide a reta r nas semi-retas e
![]() :
:
indica a semi-reta de origem em A e que passa por M;
![]() indica a semi-reta de origem em M e que passa por A.
indica a semi-reta de origem em M e que passa por A.
Pontos Colineares e Segmentos Consecutivos
Pontos que pertencem a uma mesma reta são chamados de pontos colineares.
__________________________r___
M N P
M, P e N são pontos colineares.
Dois segmentos que possuem uma extremidade em comum são chamados de segmentos consecutivos:
__ __
AB e BC são segmentos consecutivos.
Dois segmentos consecutivos podem ser:
Colineares:
_________________________r___
A B C
__ __
AB e BC são segmentos consecutivos e colineares, pois estão contidos numa mesma reta r.
Não Colineares:
__ __
AB e BC são segmentos consecutivos e não colineares, pois não estão contidos em uma mesma reta.
Congruência de Segmentos
Dois segmentos que possuem a mesma medida, são chamados congruentes.
Exemplo:
A________________________B
C________________________D
__ __ __ __
A B = C D, se lê A B congruente ao C D.
Ângulos
Considere três pontos não-colineares (que não pertencem a uma mesma reta) A, O e B.
Ângulo geométrico AÔB é a figura formada pelas semi-retas AO e OB:
Na figura:
*O ponto O é o vértice do ângulo;
*As semi-retas AO e OB são os lados do ângulo.
Instrumento para medir ângulo
O instrumento mais usado para medir ângulos é o transferidor. O transferidor tem como unidade o grau Indicamos um grau assim: 1º.
Classificação de Ângulos
A medida do ângulo é classificada assim:
| Medida do Ângulo: | Nome do Ângulo: |
| Igual a 90º | Reto |
| Maior que 90º | Obtuso |
| Menor que 90º | Agudo |
Curvas
Veja os tipos de curvas:
*Curva aberta simples: É uma curva aberta onde as linhas não se cruzam.
* Curva aberta não-simples: É uma curva aberta, porém as linhas se cruzam.
*Curva fechada simples: É uma curva fechada onde as linhas não se cruzam.
*Curva fechada não-simples: É uma curva fechada onde as linhas se cruzam.
Polígonos
As curvas fechadas simples formadas por segmento de reta recebem o nome de polígonos.
Classificação de polígonos
Os polígonos são classificados da seguinte maneira, em relação ao número de lados:
Número de lados: Nome:
3…………………………….Triângulo
4…………………………….Quadrilátero
5…………………………….Pentágono
6…………………………….Hexágono
7…………………………….Heptágono
8…………………………….Octógono
9…………………………….Eneágono
10…………………………..Decágono
11…………………………..Undecágono
12…………………………..Dodecágono
15…………………………..Pentadecágono
20…………………………..Icoságono
Os polígonos que não constam na relação acima, são chamados de polígono de treze lados, polígono de quatorze lados, polígono de dezenove lados, etc…
Elementos do Polígono
Os segmentos
![]() são os lados do polígono.
são os lados do polígono.
Os pontos A, B, C, D, E e F, pontos comuns a dois lados são os vértices do polígono.
Unindo as vértices A e C do polígono, você construí uma diagonal do polígono. As diagonais são obtidas ligando-se dois vértices não consecutivos do polígono.
No polígono A B C D E F, notamos que:
*Os ângulos formados por dois lados consecutivos são chamados de ângulos internos do polígono.
*Os ângulos formados por um lado e pelo prolongamento do lado consecutivo são os ângulos externos do polígono.
Obs.: Os prolongamentos dos lados são sempre ordenados.
Num polígono o número de lados, de vértices, de ângulos internos e externos é igual.
Em todo polígono o número de lados é igual ao número de vértices, que, por sua vez é igual ao número de ângulos internos e ângulos externos.
Perímetro do Polígono
Para calcular o perímetro de um polígono, temos de calcular a soma das medidas de seu lado.
Primeiro, somamos os 10cm com os outros 10cm, depois somamos o resultado (20cm) com os 5cm e o resultado (25cm) com os outros 5cm, e achamos o resultado 30cm. O perímetro desse retângulo é 30cm.
10+10+5+5= 30 cm.
Figuras Geométricas
Quadrado: Quadrilátero retangular cujos lados são iguais entre si e cujos ângulos são retos.
Retângulo: Quadrilátero cujos ângulos são retos e os lados opostos são iguais.
Paralelogramo: Quadrilátero plano cujos lados opostos são paralelos.
Triângulo Equilátero: O que tem três lados iguais e, portanto, os três ângulos iguais.
Triângulo Isósceles: O que tem dois lados iguais e, portanto, dois ângulos iguais.
Triângulo Retângulo: Triângulo que tem um ângulo reto.
Triângulo Escaleno: O que tem todos os ângulos e lados desiguais.
Trapézio: Quadrilátero com dois planos paralelos.
Trapézio Isósceles: Trapézio cujos lados não paralelos são iguais.
Trapézio Retângulo: Trapézio que tem dois ângulos retos.
Losango: Quadrilátero plano que tem os lados iguais, dois ângulos agudos e dois obtusos.
Círculo: Região de um plano limitado por uma circunferência.
Eclipse: Lugar Geométrico dos pontos de um plano cujas distâncias a dois pontos fixos desse plano tem soma constante.
Conjuntos
Veja o conjunto de brinquedos de Gustavo:
A bola, o peixe e o trator são elementos do conjunto.
Agora veja o conjunto A de números naturais maiores que 6 e menores que 7:
Veja que o conjunto é vazio.
Conjunto unitário é aquele que possui um só elemento, exemplo:
1) O conjunto de bolas de Gustavo.
2) Conjunto de números naturais maiores que 10 e menores que 12.
Conjunto finito é aquele que possui quantidade determinada de elementos, exemplo:
1) Conjunto de brinquedos de Gustavo.
2) Conjuntos de números pares menores que 8.
Conjunto infinito é aquele cujo número de elementos não pode ser determinado,ex:
1) Conjunto de números naturais.
Representação de conjuntos
Podemos representar o conjunto por um diagrama (curva fechada):
Escrevemos entre chaves o nome dos elementos do conjunto, separados por vírgula:
Conjunto dos Três primeiros meses do ano.
{Janeiro, fevereiro, março}
O conjunto vazio pode ser representado assim: { }
Autoria: Bruno Gruber