Os números naturais surgiram devido à necessidade de contagem. Chama-se de N o conjunto dos números naturais.
É habitual contar objetos, dinheiro, pessoas e muitas outras coisas. O conjunto dos números naturais nasceu da necessidade de contagem.
Para os matemáticos que estudam a teoria dos números, o zero não é um número natural. Aqueles, porém, que fazem estudos na área da lógica, da computação e em algumas outras áreas consideram-no número natural.
O conjunto dos números naturais é representado deste modo:
As reticências indicam que os valores seguem infinitamente.
Quando o zero é excluído da representação, indica-se da seguinte forma:
Em 1889, o matemático italiano Giuseppe Peano (1858-1932), em seu livro Arithmetices principia nova methodo exposita, estabeleceu quatro regras para a “construção” dos números naturais, conhecidas como os axiomas de Peano.
- Zero é um número.
O número zero havia surgido para preencher um espaço vazio, mas foi definitivamente elevado à categoria de número (o astrônomo indiano Brahmagupta já havia feito isso no século VII).
- Se α é um número, o sucessor de α é um número.
Isso significa que qualquer número natural possui um sucessor. Por exemplo: o sucessor de 20 é 21, o sucessor de 134 é 135 e assim por diante. Portanto, o conjunto dos números naturais possui infinitos termos.
- Não há nenhum número que tenha o zero como sucessor.
Esse axioma significa que o primeiro número natural é o zero e, portanto, ele não é sucessor de nenhum número natural e não possui nenhum antecessor. Dessa forma, estabelece-se uma ordem entre os números naturais. Por exemplo: o número 2 é menor que o número 3 (2 < 3), o número 54 é maior que o número 38 (54 > 38) e assim por diante.
- Dois números cujos sucessores são iguais são eles próprios iguais.
Esse axioma afirma, com outras palavras, que números diferentes possuem sucessores diferentes.
Representação geométrica dos números naturais
Os números naturais podem ser representados ordenadamente sobre uma reta, – de forma que se deve somar, sempre, uma unidade de medida para obter o número seguinte.
Operações:
Com os números naturais, pode-se realizar as operações de adição, multiplicação, divisão e subtração, sendo as duas últimas operações efetuadas com algumas restrições.
Soma ou adição de números naturais
Somar equivale a reunir, juntar, acumular ou acrescentar. Os termos da adição chamam-se parcelas. O resultado é a soma ou total.
Propriedades da adição:
Comutativa: a ordem das parcelas não altera a adição.
2 + 17 = 17 + 2
19 = 19
Associativa: a ordem em que se agrupam as parcelas não altera a adição.
(3 + 15) + 21 = 3 + (1.5 + 21)
18 + 21 = 3 + 36
39 = 39
Elemento neutro: é o zero. Qualquer número somado a zero é igual ao mesmo número.
56 + 0 = 56
Resto ou subtração de números naturais
Subtrair é reduzir, diminuir. Os termos da subtração chamam-se minuendo, subtraendo e resto ou diferença.
Se o minuendo for menor que o subtraendo, a subtração não terá solução no conjunto dos números naturais.
4 – 9 = ?
Em algumas expressões, aparecem de forma combinada a adição e a subtração.
Ambas as operações têm a mesma prioridade e são efetuadas na ordem em que aparecem: da esquerda para a direita.
Se aparecerem operações entre parênteses, devem-se efetuá-las em primeiro lugar.
Exemplo:
Efetuar as seguintes operações:
a) 29 + 12 – 38 + 5 = 41 – 38 + 5 = 3 + 5 = 8
b) 55 + 4 + (27 – 19) = 55 + 4 + 8 = 59 + 8 = 67
c) 37 + (52 – 18) – (67 – 29) = 37 + 34 – 38 = 71 – 38 = 33
d) 45 – 12 + (23 – 39 + 21) = 45 – 12 + (44 – 39) = 45 – 12 + 5 = 33 + 5 = 38
Multiplicação ou produto de números naturais
A multiplicação é a expressão abreviada da adição de vários termos iguais.
3 + 3 + 3 + 3 = 4 . 3 = 12
Os termos da multiplicação são denominados fatores. O resultado final é chamado de produto.
Propriedades da multiplicação:
Comutativa: a ordem dos fatores não altera o produto.
5 . 7 = 7 . 5
35 = 35
Associativa: a ordem de agrupamento dos fatores não altera o produto.
(4.7). 5 = 4 . (7.5)
28 . 5 = 4 . 35
140 = 140
Elemento neutro: é o um.
13 . 1 = 13
Distributiva: o produto de um número por uma soma ou uma diferença é igual à soma ou diferença dos produtos do número pelos termos.
4 . (8 – 3) = 4 . 8 – 4 . 3
4 . 5 = 32 – 12
20 = 20
Exemplos:
Em um cesto, há cinco sacos de batatas que “pesam” 75 kg cada um. Observar o que marca a balança:
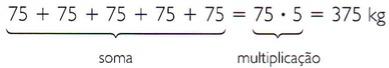
Calcular o seguinte exemplo aplicando a propriedade distributiva:
3 . (2 + 5) = 3 . 2 + 3 . 5 = 6 + 15 = 21
Divisão de números naturais
A divisão entre dois números naturais, os quais se denominam dividendo e divisor, consiste em dividir uma quantidade em partes iguais.
Quando o resto é zero, a divisão é exata. Então se tem:
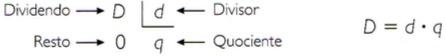
Exemplo:
Um pai quer repartir R$ 63000 entre os três filhos, em partes iguais. Quanto receberá cada um?

A divisão pode ter um resto diferente de zero. Por exemplo, ao repartir 14 bolinhas entre cinco crianças, obtém-se uma divisão com resto diferente de zero. Quando o resto é diferente de zero, a divisão é não-exata.
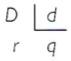
O resto (r) tem de ser um número menor que o divisor (d). Tem-se: D = d · q + r. Esse cálculo se chama prova da divisão.
Exemplo:
Uma pessoa quer repartir 43 balas entre 14 crianças. Quantas balas receberá cada criança? Quantas sobrarão?
Para comprovar que a divisão está correta, pode-se fazer a prova:
D = d · q + r onde r < d
43 = 14 – 3 + 1 r < d
43 = 42 + 1 1<14
43 = 43
Relação entre multiplicação e divisão
A multiplicação e a divisão são operações inversas.
De uma multiplicação, obtêm-se duas divisões exatas e, de uma divisão exata, uma multiplicação e outra divisão do mesmo tipo.

Por: Osvaldo Shimenes Santos