Ao longo de todo o Ensino Fundamental, temos a oportunidade de conhecer diferentes conjuntos numéricos. Neste artigo você pode relembrar todos eles, que são os conjuntos dos números naturais, inteiros, racionais, irracionais e reais.
A sequência em que esses conjuntos serão apresentados a você tem uma lógica. Afinal, nem todos foram criados em um mesmo momento histórico. Na Matemática, os conceitos, teoremas e algoritmos são desenvolvidos com base em uma espécie de ação e reação.
Conforme o homem se depara com situações novas, surge a necessidade de desenvolver novos raciocínios lógicos, símbolos, algoritmos e teoremas capazes de solucionar esses novos problemas.
Conjunto dos Números Naturais (N)
O primeiro dos conjuntos numéricos, usado quando precisamos fazer uma simples contagem e estudado ainda nas séries iniciais, é conhecido como conjunto dos números naturais e trata-se de números que representam quantidades inteiras, porém não negativas. Chama-se de N o conjuntos dos números naturais.
O conjunto dos números naturais é formado por uma sequência de números que aumentam de 1 em 1 unidade, partindo do 0 (zero):
N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, …}
Veja os principais subconjuntos de Ν:
- Ν* = conjuntos dos naturais sem o zero = {1, 2, 3, 4, 5,…}.
- Np = conjunto dos naturais pares = {0, 2, 4, 6, 8,…}.
- Ni = conjunto dos naturais ímpares = {1, 3, 5, 7, 9,…,}.
Podemos considerar o conjunto dos números naturais ordenados sobre uma reta, como mostra o gráfico abaixo:
Conjunto dos números inteiros (Z)
Em determinadas circunstâncias de nosso cotidiano, temos necessidade de usar números que sejam menores que zero, como a indicação de temperaturas, conforme os graus Celsius (°C)
Não é possível, no conjunto dos números naturais, subtrair 5 unidades de 2. Mas, e quando subtraímos 5 graus Celsius de 2 graus Celsius? Na prática, esse fato ocorre, e precisamos ampliar o conjunto para indicar um resultado para essa situação.
Nesse contexto, temos o surgimento do conjunto dos números inteiros, representado por ℤ, que além dos valores inteiros, dá conta de valores também negativos.
O conjunto dos números inteiros é definido como:
Z = {…, -4, -3, -2, -1, 0, 1, 2, 3, 4,…}
Temos também outros subconjuntos de Z:
- Z* = inteiros sem o zero = Z-{0} ou {…, –3, –2, –1, 1, 2, 3,…}
- Z+ = inteiros não negativos = {0,1,2,3,4,5,…}
- Z_ = inteiros não positivos = {0,-1,-2,-3,-4,-5,…}
Observe que Z+ = Ν.
Podemos considerar os números inteiros ordenados sobre uma reta, conforme mostra o gráfico abaixo:
Conjunto dos números racionais (Q)
Nem sempre as medidas são inteiras, sendo necessário criar a escrita de números que representam partes de inteiros.
Após muitas tentativas ao longo da história da humanidade, partindo de várias civilizações, duas formas de escrita consolidaram-se: fração e número decimal. Além delas, temos outros formatos de escrita, como a porcentagem, que são variações da escrita fracionária ou decimal.
Os números chamados racionais são representados pela divisão (razão) entre dois inteiros:
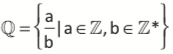
Os números racionais portanto, são todos aqueles que podem ser colocados na forma de fração (com o numerador e denominador 
Z). Ou seja, o conjunto dos números racionais é a união do conjunto dos números inteiros com as frações positivas e negativas.
Exemplos:
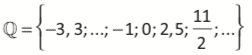
Conjunto dos números irracionais (I)
Em um simples pneu de bicicleta, podemos encontrar uma relação que faz surgir um tipo de número que intrigou muitos matemáticos há alguns milênios. Há poucos séculos, foi possível observar que esse mesmo número apresentava infinitas casas decimais, sem que se formasse um período. Em qualquer outro objeto circular, também encontramos esse número tão especial que acabou recebendo um nome específico.
Trata-se do conjunto dos números irracionais, de que são exemplos a raiz quadrada de um número primo, como raiz quadrada de 2, e o famoso número π, que é igual à razão entre as medidas do comprimento da circunferência e seu diâmetro (c/d = π ≈ 3,14).
Como exemplo de números irracionais, temos a raiz quadrada de 2 e a raiz quadrada de 3:
Conjunto dos números reais (R)
Com base em todos os conjuntos estudados até aqui, formamos um único conjunto, chamado de conjunto dos números reais, indicado por R, que é a reunião do conjunto dos números racionais com o conjunto dos números irracionais. Nesse caso, todos os pontos de uma reta podem ser representados por números reais, sendo eles racionais ou irracionais.
O diagrama abaixo mostra uma relação entre esses conjuntos:
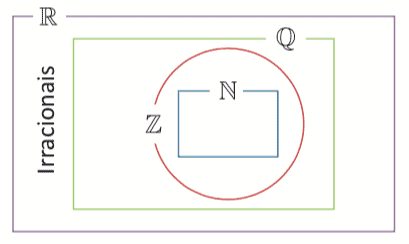
Conclui-se então que os números reais formam um conjunto numérico que abrange todos os números dos demais conjuntos numéricos estudados anteriormente. Portanto, os números naturais, inteiros, racionais e irracionais são todos números reais.
Como subconjuntos importantes de R temos:
- R* = conjunto dos números reais sem o zero = IR-{0}
- R+ = conjunto dos números reais não negativos.
- R_ = conjunto dos números reais não positivos.
Relação entre conjuntos numéricos
Perceba que certos conjuntos numéricos são subconjuntos de outros conjuntos numéricos.
- Todo número natural é também um número inteiro. Assim, dizemos que N está contido em Z (N ⊂ Z).
- Todo número inteiro é também um número racional: (Z ⊂ Q)
- Todo número racional é também um número real: (Q ⊂ R)
De maneira geral, temos:
N ⊂ Z ⊂ Q ⊂ R
Essa relação diz que o conjunto dos naturais está contido no conjunto dos inteiros, que, por sua vez, está contido no conjunto dos racionais, que está contido no conjunto dos reais. Vale lembrar que este último contém também os números irracionais
Por: Juliano Zambom Niderauer
