O máximo divisor comum de vários números é o maior de seus divisores comuns. Ele é representado pela sigla mdc (a, b, c,…) e é obtido decompondo os números em fatores primos e multiplicando tais fatores comuns elevados ao menor de seus expoentes.
Conceito de máximo divisor comum
Chama-se máximo divisor comum (mdc) de dois ou mais números o maior de seus divisores comuns.
Exemplos:
Calcular o máximo divisor comum de 48 e 32.
Encontram-se os divisores de 48 e 32 decompondo-os em fatores primos:

Os divisores comuns a ambos os números são: 1,2, 4, 8, 16.
O maior de todos eles é 16 = 24
Ele é denominado máximo divisor comum de 48 e 32 e representado da seguinte forma: mdc (48, 32) = 16.
Calcular o máximo divisor comum de 12 e 40.
- divisores de 12: {1,2, 3, 4, 6, 12}
- divisores de 40: {1,2, 4, 5, 8, 10, 20, 40}
Divisores comuns a 12 e 40: 1,2, 4.
O maior divisor comum é 4. Portanto, mdc (12, 40) = 4.
Se o único divisor comum de dois ou mais números for a unidade, esses números serão primos entre si.
Forma prática de calcular o mdc
Para calcular o máximo divisor comum de dois ou mais números:
- Decompor ó número em fatores primos.
- Expressar os números como produto de fatores primos.
- Escolher os fatores primos comuns e os fatores comuns elevados ao menor expoente.
- O produto desses fatores é o mdc dos números.
Exemplos:
- Calcular o máximo divisor comum de 40 e 100.
- Decompor em fatores primos 40 e 100.
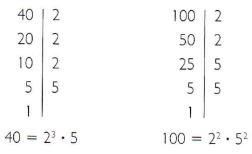
- Fatores comuns: 2 e 5.
Fatores comuns elevados aos menores expoentes: 22 e 5.
- mdc (40, 100) = 22 5 = 20.
- Calcular o máximo divisor comum de 24, 32 e 36.

- Decompor em fatores.
- Fatores comuns: 2.
Fatores comuns elevados ao menor expoente: 22.
- mdc (24, 32, 36) = 22 = 4.
Outra forma de calcular
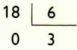
Outra forma de determinar o mdc dos números é o método das divisões sucessivas (algoritmo de Euclides). Obtém-se o mdc (24,18) usando esse método:
- Dividir 24 por 18. O quociente é 1 e o resto é 6.

- O resto 6 passa a ser o divisor do 18 (antigo divisor).

- Ao dividir 18 por 6, obtêm-se quociente 3 e resto zero.
- Quando se chega ao resto zero, o processo termina.
O último resto anterior a zero, no caso o 6, é o mdc de 24 e 18.
mdc (24, 18) = 6.