Os números primos têm como únicos divisores eles mesmos e a unidade, os números que têm outros divisores além deles mesmos e a unidade são chamados de compostos.
Números primos
Um número o será primo se tiver apenas dois divisores: ele mesmo e a unidade.
Um número primo a só pode ser expresso como produto dele mesmo pela unidade:
a = a • 1
O número 2 é primo porque só tem dois divisores: {2, 1}.
O número 2 só pode ser expresso sob a forma
2 = 2 • 1.
O número 13 é primo porque só tem dois divisores: {13, 1}.
O número 13 só pode ser expresso como 13 = 13 • 1.
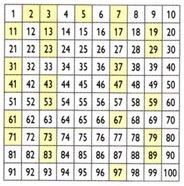
Crivo de Eratóstenes
Criado pelo matemático, geógrafo e astrônomo grego Eratóstenes (276 a.C.-194 a.C), o processo denominado crivo de Eratóstenes permite determinar os números primos menores do que certo número. Como obter os números primos menores do que 100?
Inicialmente, elimina-se o número 1. Depois, preserva-se o número 2 (o primeiro número primo) e eliminam-se todos os múltiplos de 2. Em seguida, mantém-se o número 3 e suprimem-se os múltiplos de 3. Sucessivamente, fazer o mesmo com os outros números primos. Os números que sobrarem são os números primos até o número 100.
Infinitude dos números primos (Euclides)
Segundo o matemático grego Euclides (360 a.C-295 a.C), em uma coleção finita de números primos p1, p2, p3…..pn existe sempre outro número primo que não é membro da coleção.
Euclides sugere considerar um número p, que deve ser igual ao produto de todos os números primos da coleção, acrescido de uma unidade, isto é, p = 1 + p1 • p2 • p3 • …, pn .
Como p é maior que 1, ele tem pelo menos um divisor primo, que não pode ser igual a p1, p2, p3…..pn, pois a divisão de p por quaisquer desses primos tem como resto o número 1.
Portanto, p deve ser divisível por um número primo diferente daqueles apresentados inicialmente, o qual será o próprio p. Isso significa que a coleção dos números primos é infinita.
Números compostos
Um número será composto se tiver outros divisores além dele mesmo e da unidade. Um número composto pode ser decomposto como produto de outros fatores. O número 6 é composto porque seus divisores são: {1, 2, 3, 6}. O número 1 8 é composto porque seus divisores são: {1, 2, 3, 6, 9, 18}.
O número 6 pode ser expresso como produto de fatores primos: 6 = 6 • 1 ou 6 = 2 • 3.
O número 18 pode ser expresso como produto de fatores: 18 = 1 • 18 ou 18 = 2 • 9 ou 18 = 3 • 6.
Exemplo:
Como averiguar se um número é primo ou composto?
- Deve-se dividir o número por sucessivos números primos: 2, 3, 5, 7, …
- Caso se obtenha uma divisão exata, o número será composto.
- Caso se obtenha uma divisão em que o quociente seja igual ou menor que o divisor, sem chegar previamente a uma divisão exata, o número será primo.
Como averiguar se o número 101 é primo ou composto?
- O número 101 não é divisível por 2 porque não termina em zero nem em algarismo par;
- não é divisível por 3 porque 1 +0+1 =2, que não é múltiplo de 3;
- não é divisível por 5 porque termina em 1;

O número 101 é um número primo.
Números primos entre si
Dois números serão primos entre si (ou primos relativos) se o único divisor comum de ambos for a unidade.
Exemplo:
Para verificar se os números 8 e 15 são primos entre si:
- Calcular os divisores de 8: {1, 2, 4, 8}.
- Calcular os divisores de 15: {1, 3, 5, 15}.
Como o único divisor comum de ambos é 1, 8 e 15 são números primos entre si.
Veja também:
- Fatoração – Decomposição em fatores primos
- Conjuntos Numéricos
- Números Naturais
- Números Inteiros
- Números Reais
- Números Racionais e Irracionais
- Como calcular o MDC – Máximo Divisor Comum
- Como calcular o MMC – Mínimo Múltiplo Comum